题目内容
15.方程x3-6x2+9x-10=0的实数根有1个.分析 应用导数的几何意义易判断函数的增减性,然后根据极值判断实根的个数.
解答 解:设f(x)=x3-6x2+9x-10,
则f′(x)=3x2-12x+9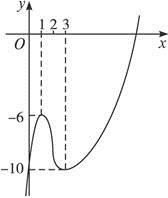 ,
,
令f′(x)=0得x1=1或x=3.
∴x≤1时,f(x)单调递增,极大值为-6;
当1<x≤3时,f(x)单调递减,极小值为-10;
当x>3时,f(x)单调递增,极小值为-10,
由上分析知y=f(x)的图象如图,与x轴只有一个公共点,
所以方程x3-6x2+9x-10=0只有一个实根.
故答案为:1.
点评 本题考查方程和函数的关系,导数的运用:求单调区间和极值,考查数形结合的数学思想,属于中档题.

练习册系列答案
相关题目
5.若角α终边在第二象限,则π-α所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
20.已知复数z满足z(1-2i)=i,则复数对应的点在复平面对应的点位于 ( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
4.已知等差数列的首项为31,若从第16项开始小于1,则此数列的公差d的取值范围是( )
| A. | (-∞,-2) | B. | [-$\frac{15}{7}$,-2) | C. | (-2,+∞) | D. | (-$\frac{15}{7}$,-2) |