题目内容
已知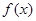
是R上最小正周期为2的周期函数，且当
时，
，则函数
在区间
上的图像与x轴的交点个数为（ ）
| A．6 | B．7 | C．8 | D．9 |
B
解析试题分析：当0≤x＜2时，令=0，则x（x-1）（x+1）=0，解得x=0或1；又f（x）是R上最小正周期为2的周期函数，∴f（0）=f（2）=f（4）=f（6）=0，f（1）=f（3）=f（5）=0，故在区间[0，6]上，方程f（x）=0共有7个根，∴函数y=f（x）的图象在区间[0，6]上与x轴的交点的个数为7．故选B．
考点：本题考查了根的存在性及根的个数判断．
点评：正确求出一个周期内的根的个数和理解周期性是解题的关键
练习册系列答案
相关题目
已知定义域为
的偶函数
在
上是减函数，且
，则不等式
（ ）
A． | B． | C． | D． |
已知函数
中，常数
那么
的解集为
A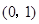． | B． | C． | D． |
下列函数中，在区间
上为减函数的是（ ）
A． | B． | C． | D． |
已知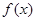
在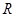
上是减函数，则满足
＞
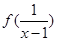的实数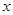
的取值范围是( )．
| A．(－∞，1) | B．(2，＋∞) |
| C．(－∞，1)∪(2，＋∞) | D．(1，2) |
函数
＋1（a＞0，a≠1）的图象必经过定点 （ ）
| A．（0，1） | B．（2，1） | C．（2，2） | D．（2，3） |
已知函数
，,则函数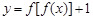
的零点个数是
| A．4 | B．3 | C．2 | D．1 |
若a是函数
的零点，若
，则
的值满足
A． | B． | C． | D．的符号不确定 |
函数
在区间
单调递增，则实数
的取值范围为
A． | B． | C． | D． |