题目内容
已知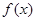 在
在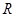 上是减函数,则满足
上是减函数,则满足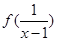 >
> 的实数
的实数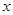 的取值范围是( ).
的取值范围是( ).
| A.(-∞,1) | B.(2,+∞) |
| C.(-∞,1)∪(2,+∞) | D.(1,2) |
C
解析试题分析:因为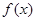 在
在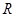 上是减函数,所以由
上是减函数,所以由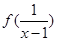 >
> 可知
可知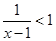 ,解得实数
,解得实数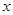 的取值范围是(-∞,1)∪(2,+∞).
的取值范围是(-∞,1)∪(2,+∞).
考点:本小题主要考查函数单调性的应用.
点评:应用函数的单调性解抽象不等式,关键是根据函数的单调性去掉 ,然后求解不等式时要求解正确.
,然后求解不等式时要求解正确.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
函数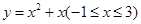 的值域是( )
的值域是( )
A. | B.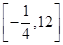 | C. | D.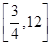 |
若函数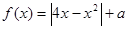 有4个零点,则实数
有4个零点,则实数 的取值范围是( )
的取值范围是( )
A.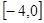 | B.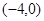 | C.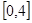 | D.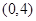 |
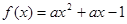 在
在 上恒满足
上恒满足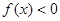 ,则
,则 的取值范围是
的取值范围是
A.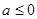 | B.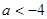 | C.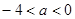 | D.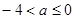 |
已知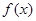 是R上最小正周期为2的周期函数,且当
是R上最小正周期为2的周期函数,且当 时,
时, ,则函数
,则函数 在区间
在区间 上的图像与x轴的交点个数为( )
上的图像与x轴的交点个数为( )
| A.6 | B.7 | C.8 | D.9 |
已知函数 ,则函数
,则函数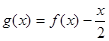 的零点个数为
的零点个数为
| A.1 | B.2 | C.3 | D.4 |
方程 的根所在区间为 ( )
的根所在区间为 ( )
A.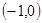 | B. | C.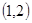 | D.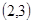 |
若函数f (x) = x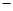
 在[1,+∞)上是增函数,则实数p的取值范围是( )
在[1,+∞)上是增函数,则实数p的取值范围是( )
A. | B. | C. | D. |
给出以下结论:①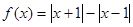 是奇函数;②
是奇函数;②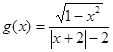 既不是奇函数也不是偶函数;③
既不是奇函数也不是偶函数;③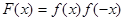
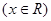 是偶函数 ;④
是偶函数 ;④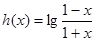 是奇函数.其中正确的有( )个
是奇函数.其中正确的有( )个
| A.1个 | B.2个 | C.3个 | D.4个 |