题目内容
已知函数 ,,则函数
,,则函数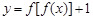 的零点个数是
的零点个数是
| A.4 | B.3 | C.2 | D.1 |
A
解析试题分析:根据题意,由于函数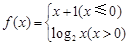 ,那么可知函数
,那么可知函数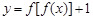 的零点,即为f(f(x)+1=0的解得个数,因为结合图像可知,满足f(f(x)=-1,则可知f(x)=-2,或者f(x)=
的零点,即为f(f(x)+1=0的解得个数,因为结合图像可知,满足f(f(x)=-1,则可知f(x)=-2,或者f(x)=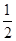 ,因此可知满组每个方程的解有2个,则可知解有4个,故选A.。
,因此可知满组每个方程的解有2个,则可知解有4个,故选A.。
考点:函数零点
点评:解决函数零点的问题,一般考查运用数形结合思想来解答,属于中档题。

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
函数f(x)=2x+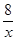 (x>0)有
(x>0)有
| A.最大值8 | B.最小值8 | C.最大值4 | D.最小值4 |
若函数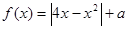 有4个零点,则实数
有4个零点,则实数 的取值范围是( )
的取值范围是( )
A.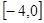 | B.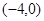 | C.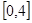 | D.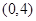 |
已知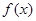 是R上最小正周期为2的周期函数,且当
是R上最小正周期为2的周期函数,且当 时,
时, ,则函数
,则函数 在区间
在区间 上的图像与x轴的交点个数为( )
上的图像与x轴的交点个数为( )
| A.6 | B.7 | C.8 | D.9 |
已知函数 ,则函数
,则函数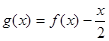 的零点个数为
的零点个数为
| A.1 | B.2 | C.3 | D.4 |
已知函数 ,则该函数是 ( )
,则该函数是 ( )
A.偶函数,且单调递增  | B.偶函数,且单调递减 |
| C.奇函数,且单调递增 | D.奇函数,且单调递减 |
方程 的根所在区间为 ( )
的根所在区间为 ( )
A.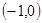 | B. | C.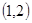 | D.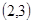 |
设偶函数f(x)的定义域为R,当x 时f(x)是增函数,则f(-2),f(
时f(x)是增函数,则f(-2),f( ),f(-3)的大小关系是:( )
),f(-3)的大小关系是:( )
A.f( )>f(-3)>f(-2) )>f(-3)>f(-2) | B.f( )>f(-2)>f(-3) )>f(-2)>f(-3) |
C.f( )<f(-3)<f(-2) )<f(-3)<f(-2) | D.f( )<f(-2)<f(-3) )<f(-2)<f(-3) |
 是函数
是函数 的导函数,
的导函数, 的图象如图所示,则
的图象如图所示,则 的图象最有可能的是( )
的图象最有可能的是( )