题目内容
已知函数 中,常数
中,常数 那么
那么 的解集为
的解集为
A.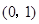 | B. | C. | D. |
B
解析试题分析:由题意可得:令u(x)=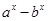 ,不等式即 lgu(x)>0,
,不等式即 lgu(x)>0,
∵a>1>b>0,
所以u(x)在实数集上是个增函数,且u(x)>0,
又因为u(0)=0,
所以应有 x>0,
∴u(x)在定义域(0,+∞)上单调增,
∴f(x)=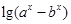 在x∈(0,+∞)上单调增.
在x∈(0,+∞)上单调增.
又f(1)=lg(a-b)=lg1=0,由f(x)>0知x>1.
故选B.
考点:指数函数与对数函数的单调性
点评:本题考查指数函数、对数函数的单调性与特殊点,由真数u(x)的单调性确定f(x)的单调性,利用特殊点lg1=0.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
函数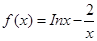 的零点所在的大致区间是( )
的零点所在的大致区间是( )
A.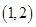 | B.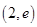 |
C. | D.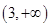 |
函数f(x)=2x+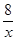 (x>0)有
(x>0)有
| A.最大值8 | B.最小值8 | C.最大值4 | D.最小值4 |
关于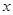 的方程
的方程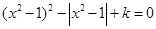 ,给出下列四个命题:
,给出下列四个命题:
①存在实数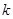 ,使得方程恰有2个不同实根; ②存在实数
,使得方程恰有2个不同实根; ②存在实数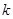 ,使得方程恰有4个不同实根;
,使得方程恰有4个不同实根;
③存在实数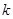 ,使得方程恰有5个不同实根; ④存在实数
,使得方程恰有5个不同实根; ④存在实数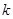 ,使得方程恰有8个不同实根;
,使得方程恰有8个不同实根;
其中假命题的个数是( )
| A.0 | B.1 | C.2 | D.3 |
函数 ( )
( )
A.是奇函数,且在 上是单调增函数 上是单调增函数 |
B.是奇函数,且在 上是单调减函数 上是单调减函数 |
C.是偶函数,且在 上是单调增函数 上是单调增函数 |
D.是偶函数,且在 上是单调减函数 上是单调减函数 |
若函数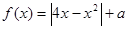 有4个零点,则实数
有4个零点,则实数 的取值范围是( )
的取值范围是( )
A.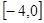 | B.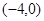 | C.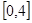 | D.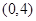 |
已知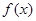 是R上最小正周期为2的周期函数,且当
是R上最小正周期为2的周期函数,且当 时,
时, ,则函数
,则函数 在区间
在区间 上的图像与x轴的交点个数为( )
上的图像与x轴的交点个数为( )
| A.6 | B.7 | C.8 | D.9 |
给出以下结论:①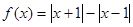 是奇函数;②
是奇函数;②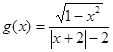 既不是奇函数也不是偶函数;③
既不是奇函数也不是偶函数;③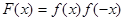
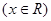 是偶函数 ;④
是偶函数 ;④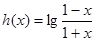 是奇函数.其中正确的有( )个
是奇函数.其中正确的有( )个
| A.1个 | B.2个 | C.3个 | D.4个 |
 是函数
是函数 的导函数,
的导函数, 的图象如图所示,则
的图象如图所示,则 的图象最有可能的是( )
的图象最有可能的是( )