题目内容
4.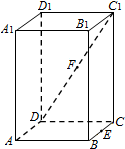 在正四棱柱ABCD-A1B1C1D1中,E是BC的中点,F是C1D的中点,P是棱CC1所在直线上的动点.则下列四个命题:
在正四棱柱ABCD-A1B1C1D1中,E是BC的中点,F是C1D的中点,P是棱CC1所在直线上的动点.则下列四个命题:①CD⊥PE
②EF∥平面ABC1
③${V_{P-{A_1}D{D_1}}}={V_{{D_1}-ADE}}$
④不存在过P的直线与正四棱柱的各个面都成等角.
其中正确命题的序号是①③(写出所有正确命题的序号).
分析 根据标榜的结构特征,结合线面垂直的判定与性质,面面平行的判定与性质,锥体的体积公式,直线与平面的夹角等知识点,分别判断4个结论的真假,可得答案.
解答  解:在①中:∵正四棱柱ABCD-A1B1C1D1中,E是BC的中点,F是C1D的中点,P是棱CC1所在直线上的动点,
解:在①中:∵正四棱柱ABCD-A1B1C1D1中,E是BC的中点,F是C1D的中点,P是棱CC1所在直线上的动点,
∴CD⊥平面ECC1,又PE?平面ECC1,∴CD⊥PE,故①正确;
在②中:EF?平面EC1D,延长C1E与B1B交于H,连接DH,得DH平行于EF,
DH与平面ABC1相交,故②EF∥平面ABC1不正确;
在③中:${V}_{P-{A}_{1}D{D}_{1}}$=$\frac{1}{6}$${V}_{ABCD-{A}_{1}{B}_{1}{C}_{1}{D}_{1}}$,${V}_{{D}_{1}-ADE}$=$\frac{1}{6}$${V}_{ABCD-{A}_{1}{B}_{1}{C}_{1}{D}_{1}}$,
故③${V_{P-{A_1}D{D_1}}}={V_{{D_1}-ADE}}$正确;
在④中:过P做一条与以ABCD为底面的正方体的对角线平行的直线,
则该直线与正四棱柱的各个面都成等角.故④不正确;
故正确命题的序号为:①③.
故答案为:①③.
点评 本题考查的知识点是线面垂直的判定与性质,面面平行的判定与性质,锥体的体积公式,直线与平面的夹角,是立体几何知识的综合考查,是中档题.

练习册系列答案
相关题目
14.抛物线$y=\frac{1}{8}{x^2}$的焦点到双曲线${y^2}-\frac{x^2}{3}=1$的一条渐近线的距离为( )
| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | $2\sqrt{3}$ |
15.已知函数f(x)=$\left\{\begin{array}{l}{{e}^{x},x<0}\\{x+m,x≥0}\end{array}\right.$,以下说法正确的是( )
| A. | ?m∈R,函数f(x)在定义域上单调递增 | B. | ?m∈R,函数f(x)存在零点 | ||
| C. | ?m∈R,函数f(x)有最大值 | D. | ?m∈R,函数f(x)没有最小值 |
19.某中学采用系统抽样方法,从该校高一年级全体500名学生中抽50名学生做牙齿健康检查.现将500名学生从1到500进行编号.已知从21~30这10个数中取的数是24,则在第1小组1~10中随机抽到的数是( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
9.已知$\overrightarrow{AB}$=(-1,-2),$\overrightarrow{BC}$=(-3,-4),则$\overrightarrow{CA}$=( )
| A. | (4,6) | B. | (-4,-6) | C. | (2,2) | D. | (-2,-2) |
13.已知实数x、y、z满足x2+y2+z2=4,则(2x-y)2+(2y-z)2+(2z-x)2的最大值是( )
| A. | 12 | B. | 20 | C. | 28 | D. | 36 |
14.关于x的不等式$\frac{2x-3a}{x+2a}≤1(a<0)$的解集是( )
| A. | [5a,-2a) | B. | (-∞,5a]∪(-2a,+∞) | C. | (-2a,5a]? | D. | (-∞,5a] |
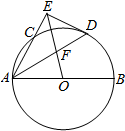 如图,AB是圆O的直径,AC是弦,∠BAC的平分线AD交圆O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F.
如图,AB是圆O的直径,AC是弦,∠BAC的平分线AD交圆O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F.