题目内容
9.直线x-2y+2=0经过椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$(a>0,b>0)的两个顶点.(1)求椭圆C的方程;
(2)已知抛物线D:y=x2+$\frac{1}{4}$,点M在抛物线D上运动,直线l:y=x+m(m∈[-$\sqrt{2}$,-1])交椭圆C于点N,P,求△MNP面积的最小值.
分析 (1)直线x-2y+2=0与坐标轴的交点为(-2,0),(0,1),即可得出a,b,可得椭圆方程.
(2)对于确定的一条直线l,作与l平行且与抛物线相切的直线n,直线n与抛物线相切的切点为M,此时△MNP面积为最小.设直线n的方程为:y=x+n,与椭圆方程联立得到:${x}^{2}-x-n+\frac{1}{4}$=0,令△=0,解得n=0.直线l与直线n的距离为d=$\frac{|m|}{\sqrt{2}}$=$\frac{-m}{\sqrt{2}}$.由$\left\{\begin{array}{l}{y=x+m}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,可得:5x2+8mx+4m2-4=0,设N(x1,y1),P(x2,y2).利用根与系数的关系可得|NP|=$\sqrt{2[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$.S△MNP=$\frac{1}{2}$|NP|•d,根据m的取值范围即可得出.
解答 解:(1)直线x-2y+2=0与坐标轴的交点为(-2,0),(0,1),
∴a=2,b=1.
∴椭圆方程为:$\frac{{x}^{2}}{4}+{y}^{2}$=1.
(2)对于确定的一条直线l,作与l平行且与抛物线相切的直线n,直线n与抛物线相切的切点为M,此时△MNP面积为最小.
设直线n的方程为:y=x+n,
联立$\left\{\begin{array}{l}{y=x+n}\\{y={x}^{2}+\frac{1}{4}}\end{array}\right.$,得到:${x}^{2}-x-n+\frac{1}{4}$=0,
则△=1-4$(\frac{1}{4}-n)$=0,解得n=0.
直线l与直线n的距离为d=$\frac{|m|}{\sqrt{2}}$=$\frac{-m}{\sqrt{2}}$.
设N(x1,y1),P(x2,y2).
由$\left\{\begin{array}{l}{y=x+m}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,可得:5x2+8mx+4m2-4=0,
∴x1+x2=$\frac{-8m}{5}$,x1x2=$\frac{4{m}^{2}-4}{5}$.
则|NP|=$\sqrt{2[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$=$\sqrt{\frac{2[64{m}^{2}-20(4{m}^{2}-4)]}{5}}$=$\frac{4\sqrt{2}}{5}\sqrt{5-{m}^{2}}$.
∴S△MNP=$\frac{1}{2}$|NP|•d=$\frac{1}{2}•$$\frac{4\sqrt{2}}{5}\sqrt{5-{m}^{2}}$×$\frac{-m}{\sqrt{2}}$=$\frac{2}{5}\sqrt{5{m}^{2}-{m}^{4}}$
=$\frac{2}{5}\sqrt{-({m}^{2}-\frac{5}{2})^{2}+\frac{25}{4}}$,
∵$m∈[-\sqrt{2},-1]$,∴m2∈[1,2].
∴当m2=1时,(S△MNP)=$\frac{4}{5}$.
点评 本题考查了椭圆与抛物线的标准方程及其性质、直线与椭圆相交问题、直线与抛物线相切问题、三角形的面积计算公式,考查了推理能力与计算能力,属于难题.

 春雨教育同步作文系列答案
春雨教育同步作文系列答案| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | $2\sqrt{3}$ |
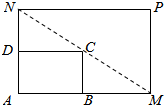 如所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,使点M,N分别在AB,AD的延长线上,且对角线MN过点C,已知AB=2米,AD=3米.
如所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,使点M,N分别在AB,AD的延长线上,且对角线MN过点C,已知AB=2米,AD=3米. 如图,已知圆G:x2+y2-2x-$\sqrt{2}$y=0经过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点F及上顶点B,过椭圆外一点(m,0)(m>a)且倾斜角为$\frac{5}{6}$π的直线l交椭圆于C,D两点.
如图,已知圆G:x2+y2-2x-$\sqrt{2}$y=0经过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点F及上顶点B,过椭圆外一点(m,0)(m>a)且倾斜角为$\frac{5}{6}$π的直线l交椭圆于C,D两点.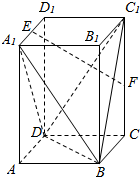 在正棱柱ABCD一A1B1C1D1中,AA1=2AB,若E,F分别为线段A1D1,CC1的中点.求:
在正棱柱ABCD一A1B1C1D1中,AA1=2AB,若E,F分别为线段A1D1,CC1的中点.求: 如图所示,四边形ABCD是正方形,PA⊥平面ABCD,且PA=AB.
如图所示,四边形ABCD是正方形,PA⊥平面ABCD,且PA=AB.