题目内容
3.函数y=$\frac{1}{4{-2}^{x}}$关于点(2,$\frac{1}{8}$)对称.分析 设函数y=$\frac{1}{4{-2}^{x}}$关于点P(a,b)对称,点A(x,y)是f(x)=$\frac{1}{4{-2}^{x}}$的图象上一点,利用对称性求出与A与关于点P对称的点A′的坐标,分别代入函数解析式化简后,利用纵坐标相等列出方程,利用系数相等列出方程组求出a、b的值.
解答 解:设函数y=$\frac{1}{4{-2}^{x}}$关于点P(a,b)对称,
∵f(x)=$\frac{1}{4{-2}^{x}}$的图象关于点P对称,设点A(x,y)是f(x)=$\frac{1}{4{-2}^{x}}$的图象上一点,
∴f(x)=$\frac{1}{4{-2}^{x}}$的图象必有一点A′(x′,y′),使得点A与点A′关于点P对称,
即x+x′=2a,y+y′=2b,
∴x′=2a-x,y′=2b-y,
∵y=f(x)=$\frac{1}{4{-2}^{x}}$,y′=f(x′)=$\frac{1}{4{-2}^{x′}}$=$\frac{1}{4{-2}^{2a-x}}$=$\frac{{2}^{x}}{{2}^{x+2}{-2}^{2a}}$,
又y′=2b-y=2b-$\frac{1}{4{-2}^{x}}$=$\frac{8b-1-b•{2}^{x+1}}{4{-2}^{x}}$,
∴$\frac{8b-1-b•{2}^{x+1}}{4{-2}^{x}}$=$\frac{{2}^{x}}{{2}^{x+2}{-2}^{2a}}$=$\frac{{-2}^{x}}{{2}^{2a}{-2}^{x+2}}$=$\frac{{-2}^{x}}{{4(2}^{2a-2}{-2}^{x})}$,
则$\frac{8b-1-b•{2}^{x+1}}{4{-2}^{x}}$=$\frac{{-2}^{x}}{{4(2}^{2a-2}{-2}^{x})}$=$\frac{{-\frac{1}{4}•2}^{x}}{{2}^{2a-2}{-2}^{x}}$,所以$\left\{\begin{array}{l}{8b-1=0}\\{-2b=-\frac{1}{4}}\\{2a-2=2}\end{array}\right.$,解得a=2,b=$\frac{1}{8}$,
∴点P的坐标为(2,$\frac{1}{8}$),
故答案为:(2,$\frac{1}{8}$).
点评 本题考查函数图象关于中心对称的性质,以及对称中心的坐标求法,考查化简、变形能力,方程思想.

 名校课堂系列答案
名校课堂系列答案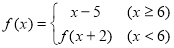 ,则
,则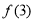 为
为