题目内容

1．函数y=$\frac{1}{x-2}$的图象与函数y=2sinπx（-1≤x≤5）的图象所有交点的横坐标之和等于（　　）
A．12B．4C．16D．8

分析 分别作出两个函数的图象，根据图象的对称性即可得到交点坐标问题．

解答 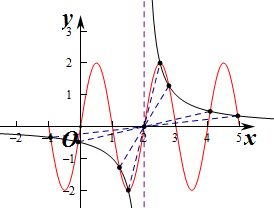解：作出函数y=$\frac{1}{x-2}$的图象，则函数关于点（2，0）对称，
同时点（2，0）也是函数y=2sinπx（-1≤x≤5）的对称点，
由图象可知，两个函数在[-1，5]上共有8个交点，两两关于点（2，0）对称，
设对称的两个点的横坐标分别为x1，x2，
则x1+x2=2×2=4，
∴8个交点的横坐标之和为4×4=16．
故选：C．

点评 本题主要考查函数交点个数以及数值的计算，根据函数图象的性质，利用数形结合是解决此类问题的关键，综合性较强．

练习册系列答案
相关题目
11．定义在（-∞，+∞）上的偶函数f（x）满足f（x+1）=-f（x），且在[-1，0]上是增函数，下面是关于f（x）的判断：
①f（8）=f（0）
②f（x）在[0，1]上是增函数；
③f（x）的图象关于直线x=1对称
④f（x）关于点P（$\frac{1}{2}，0$）对称．
其中正确的判断是①③④．
12．设不等式x2+y2≤2确定的平面区域为U，|x|+|y|≤1确定的平面区域为V（Ⅰ）定义坐标为整数的点为整点
（1）在区域U内任取1个整点P（x，y），求满足x+y≥0的概率
（2）在区域U内任取2个整点，求这两个整点中恰有1个整点在区域V内的概率
（3）在区域U内任取一个点，求此点在区域V的概率．
9．函数f（x）=sin$\frac{2x}{3}$+cos（$\frac{2x}{3}$-$\frac{π}{6}$）图象的相邻两条对称轴之间的距离等于$\frac{3π}{2}$．
16．具有性质：f（$\frac{1}{x}$）=-f（x）的函数，我们称为满足“倒负”变换的函数，下列函数：
（1）f（x）=x-$\frac{1}{x}$；
（2）f（x）=x+$\frac{1}{x}$；
（3）f（x）=$\left\{\begin{array}{l}{x，0＜x＜1}\\{0，x=1}\\{-\frac{1}{x}，x＞1}\end{array}\right.$
（4）f（x）=$\frac{1}{x}$ 
（5）f（x）=-x+$\frac{1}{{x}^{2}}$，其中满足“倒负”变换的函数是（1），（3）．．
6．已知向量$\overrightarrow a，\overrightarrow b$满足：$|{\overrightarrow a}|=1，|{\overrightarrow b}|=2$，$\overrightarrow a$与$\overrightarrow b$的夹角为$\frac{π}{3}$，则$|{2\overrightarrow a-\overrightarrow b}|$=（　　）
A．2B．4C．2$\sqrt{2}$D．8
13．三角形的周长为31，三边为a，b．c均为整数且a≤b≤c，则满足条件的三元数组（a，b，c）的个数为（　　）
A．24B．30C．48D．60
10．下面有四个命题：
①函数y=sin4x-cos4x的最小正周期是π；
②（$\overrightarrow{AB}$-$\overrightarrow{CD}$）-（$\overrightarrow{AC}$-$\overrightarrow{BD}$）=$\overrightarrow{0}$
③把函数y=3sin（2x+$\frac{π}{3}$）的图象向右平移$\frac{π}{6}$个单位长度得到y=3sin2x的图象；
④等差数列{an}的前m项和为30，前2m项和为100，则它的前3m项和为170．
其中真命题的编号是①③（写出所有真命题的编号）
11．已知函数f（x）是定义在R上的偶函数，对任意的x∈R都有f（x+4）=f（x）+2f（2），且f（-1）=2，那么f（2015）=2．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网