Question

【题目】已知函数f（x）=x3﹣ ax2 ， 且关于x的方程f（x）+a=0有三个不等的实数根，则实数a的取值范围是（ ）
A.（﹣∞，﹣ ）∪（0， ）
B.（﹣ ，0）∪（ ，+∞）
C.（﹣ ， ）
D.（﹣∞，﹣ ）∪（ ，+∞）

Answer 1

【答案】D
【解析】解：令g（x）=f（x）+a=x3﹣ ax2+a，
得g′（x）=3x2﹣3ax=3x（x﹣a），
当a=0时，g′（x）≥0，函数g（x）为增函数，不合题意；
当a＜0时，x∈（﹣∞，a），（0，+∞）时，g′（x）＞0；x∈（a，0）时，g′（x）＜0．
∴x∈（﹣∞，a），（0，+∞）时，g（x）单调递增；x∈（a，0）时，g（x）单调递减，
∴x=a时函数有极大值为g（a）= ，x=0时函数有极小值为g（0）=a．
由 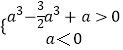，解得a ；
当a＞0时，x∈（﹣∞，0），（a，+∞）时，g′（x）＞0；x∈（0，a）时，g′（x）＜0．
∴x∈（﹣∞，0），（a，+∞）时，g（x）单调递增；x∈（0，a）时，g（x）单调递减，
∴x=0时函数有极大值为g（0）=a，x=a时函数有极小值为g（a）= ．
由 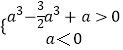，解得a ．
综上，实数a的取值范围是（﹣∞，﹣ ）∪（ ，+∞）．
故选：D．