题目内容
已知双曲线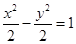 的准线过椭圆
的准线过椭圆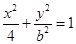 的焦点,则直线
的焦点,则直线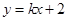 与
与
椭圆至多有一个交点的充要条件是
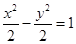 的准线过椭圆
的准线过椭圆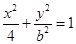 的焦点,则直线
的焦点,则直线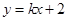 与
与椭圆至多有一个交点的充要条件是
A.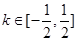 | B.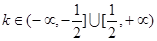 |
C.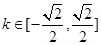 | D.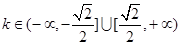 |
A
先求得准线方程,可推知a和b的关系,进而根据c2=a2-b2求得b,椭圆的方程可得,与直线y=kx+2联立消去y,根据判别式小于等于0求得k的范围.
解:根据题意,易得准线方程是x=±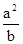 =±1
=±1
所以c2=a2-b2=4-b2=1即b2=3
所以方程是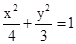
联立y=kx+2可得3x2+(4k2+16k)x+4=0
由△≤0解得K∈[-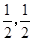 ]
]
故选A
解:根据题意,易得准线方程是x=±
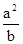 =±1
=±1所以c2=a2-b2=4-b2=1即b2=3
所以方程是
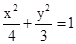
联立y=kx+2可得3x2+(4k2+16k)x+4=0
由△≤0解得K∈[-
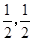 ]
]故选A

练习册系列答案
相关题目
 在区间(4,+∞)上单调递增;q:loga2<1,如果“┐p”是真命题,q也是真命题,求实数a的取值范围.
在区间(4,+∞)上单调递增;q:loga2<1,如果“┐p”是真命题,q也是真命题,求实数a的取值范围. 的充分不必要条件
的充分不必要条件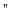
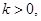 方程
方程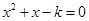 有实根”的否定是:
有实根”的否定是: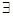
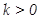 ,方程
,方程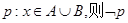 是
是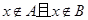
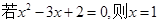 ”的逆否命题为“
”的逆否命题为“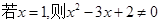 ”
”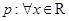 ,函数
,函数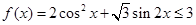 ,则
,则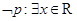 ,
,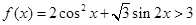
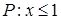 ,条件
,条件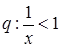 ,则
,则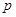 是
是
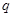 成立的 ( )
成立的 ( )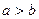 ,则
,则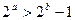 ”的否命题为______
”的否命题为______ 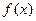 是定义在R上的偶函数,且对任意的
是定义在R上的偶函数,且对任意的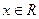 恒有
恒有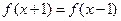 ,
,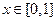 时,
时,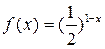 ,则其中所有正确命题的序号
,则其中所有正确命题的序号 是_____________。
是_____________。 ① 2是函数
① 2是函数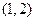 上是减函数,在
上是减函数,在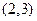 上是增函数;
上是增函数; 最
最 大值是1,最小值是0;④当
大值是1,最小值是0;④当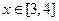 时,
时,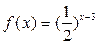 。
。