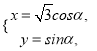题目内容
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() (θ为参数),将
(θ为参数),将![]() 上的所有点的横坐标、纵坐标分别伸长为原来的
上的所有点的横坐标、纵坐标分别伸长为原来的![]() 和2倍后得到曲线
和2倍后得到曲线![]() ,以平面直角坐标系
,以平面直角坐标系![]() 的原点
的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线
轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线![]() .
.
(1)试写出曲线![]() 的极坐标方程与曲线
的极坐标方程与曲线![]() 的参数方程;
的参数方程;
(2)在曲线![]() 上求一点
上求一点![]() ,使点
,使点![]() 到直线
到直线![]() 的距离最小,并求此最小值.
的距离最小,并求此最小值.
【答案】(1)![]() 的极坐标方程为
的极坐标方程为![]() ,
, ![]() 的参数方程是
的参数方程是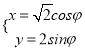 (
(![]() 是参数);(2)
是参数);(2)![]() ),最小值是
),最小值是![]() .
.
【解析】试题分析:(1)先将![]() 的参数方程化为普通方程,从而得到
的参数方程化为普通方程,从而得到![]() 的极坐标方程;先根据函数图象的伸缩变换规律得到曲线
的极坐标方程;先根据函数图象的伸缩变换规律得到曲线![]() 的普通方程,从而得到
的普通方程,从而得到![]() 的参数方程;(2)先求得直线
的参数方程;(2)先求得直线![]() 的普通方程,再利用点到直线的距离公式表示出距离,然后利用三角函数的图象与性质求得最值.
的普通方程,再利用点到直线的距离公式表示出距离,然后利用三角函数的图象与性质求得最值.
试题解析:(1)由已知得曲线![]() 的普通方程是
的普通方程是![]() ,所以
,所以![]() 的极坐标方程为
的极坐标方程为![]() .
.
根据已知的伸缩变换得曲线![]() 的普通方程是
的普通方程是![]() ,
,
所以曲线![]() 的参数方程是
的参数方程是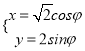 (
(![]() 是参数).
是参数).
(2)设![]() ,直线
,直线![]() 的普通方程是
的普通方程是![]() ,
,
点![]() 到直线
到直线![]() 的距离
的距离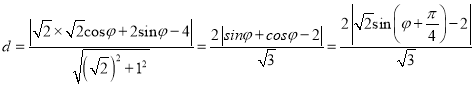 .
.
当![]() ,即
,即![]() 时,
时, 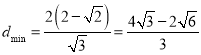 ,
,
此时点![]() 的坐标是
的坐标是![]() ,
,
所以曲线![]() 上的一点
上的一点![]() )到直线
)到直线![]() 的距离最小,最小值是
的距离最小,最小值是![]() .
.

 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案【题目】在一次抽样调查中测得样本的6组数据,得到一个变量![]() 关于
关于![]() 的回归方程模型,其对应的数值如下表:
的回归方程模型,其对应的数值如下表:
| 2 | 3 | 4 | 5 | 6 | 7 |
|
|
|
|
|
|
|
(1)请用相关系数![]() 加以说明
加以说明![]() 与
与![]() 之间存在线性相关关系(当
之间存在线性相关关系(当![]() 时,说明
时,说明![]() 与
与![]() 之间具有线性相关关系);
之间具有线性相关关系);
(2)根据(1)的判断结果,建立![]() 关于
关于![]() 的回归方程并预测当
的回归方程并预测当![]() 时,对应的
时,对应的![]() 值为多少(
值为多少(![]() 精确到
精确到![]() ).
).
附参考公式:回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为:
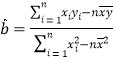 ,
,![]() ,相关系数
,相关系数![]() 公式为:
公式为: .
.
参考数据:
![]() ,
,![]() ,
,![]() ,
,![]() .
.
【题目】某研究性学习小组对春季昼夜温差大小与某花卉种子发芽多少之间的关系进行研究,他们分别记录了3月1日至3月5日的每天昼夜温差与实验室每天每100颗种子浸泡后的发芽数,得到如下资料:
日期 | 3月1日 | 3月2日 | 3月3日 | 3月4日 | 3月5日 |
温差 | 10 | 11 | 13 | 12 | 8 |
发芽数 | 23 | 25 | 30 | 26 | 16 |
(1)从3月1日至3月5日中任选2天,记发芽的种子数分别为![]() ,求事件“
,求事件“![]() 均小于25”的概率;
均小于25”的概率;
(2)请根据3月2日至3月4日的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)所得的线性回归方程是否可靠?
(参考公式:回归直线方程为![]() ,其中
,其中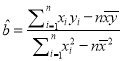 ,
, ![]() )
)
【题目】某校计划面向高一年级1240名学生开设校本选修课程,为确保工作的顺利实施,按性别进行分层抽样,现抽取124名学生对社会科学类、自然科学类这两大类校本选修课程进行选课意向调查,其中男生有65人.在这124名学生中选修社会科学类的男生有22人、女生有40人.
(1)根据以上数据完成下列列联表;
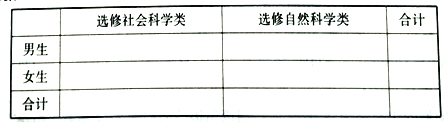
(2)判断能否有99.9%的把握认为科类的选修与性别有关?
附: 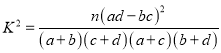 ,其中
,其中![]()
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
【题目】随着智能手机的发展,微信越来越成为人们交流的一种方式,某机构对使用微信交流的态度进行调查,随机调查了50人,他们年龄的频数分布及对使用微信交流赞成人数如表:
年龄(岁) |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(1)由以上统计数据填写下面![]() 列联表,并判断是否有99%的把握认为年龄45岁为分界点对使用微信交流的态度有差异;
列联表,并判断是否有99%的把握认为年龄45岁为分界点对使用微信交流的态度有差异;
年龄不低于45岁的人 | 年龄低于45岁的人 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(2)若对年龄分别在![]() ,
, ![]() 的被调查人中各抽取一人进行追踪调查,求选中的2人中至少有一人赞成使用微信交流的概率.
的被调查人中各抽取一人进行追踪调查,求选中的2人中至少有一人赞成使用微信交流的概率.
参考公式: ![]() ,其中
,其中![]()
参考数据:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |