题目内容
【题目】随着智能手机的发展,微信越来越成为人们交流的一种方式,某机构对使用微信交流的态度进行调查,随机调查了50人,他们年龄的频数分布及对使用微信交流赞成人数如表:
年龄(岁) |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 5 | 10 | 12 | 7 | 2 | 1 |
(1)由以上统计数据填写下面![]() 列联表,并判断是否有99%的把握认为年龄45岁为分界点对使用微信交流的态度有差异;
列联表,并判断是否有99%的把握认为年龄45岁为分界点对使用微信交流的态度有差异;
年龄不低于45岁的人 | 年龄低于45岁的人 | 合计 | |
赞成 | |||
不赞成 | |||
合计 |
(2)若对年龄分别在![]() ,
, ![]() 的被调查人中各抽取一人进行追踪调查,求选中的2人中至少有一人赞成使用微信交流的概率.
的被调查人中各抽取一人进行追踪调查,求选中的2人中至少有一人赞成使用微信交流的概率.
参考公式: ![]() ,其中
,其中![]()
参考数据:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
【答案】(I)见解析;(Ⅱ)见解析
【解析】试题分析:(I)由题意,完成 2×2 列联表,利用独立性检验的公式,求解![]() 的值,对比,即可得出结论;
的值,对比,即可得出结论;
(Ⅱ)根据题意,确定随机变量![]() 的所有可能取值,根据相互独立事件的概率公式求解相应的概率,列出分布列,代入期望的公式,即可求解数学期望.
的所有可能取值,根据相互独立事件的概率公式求解相应的概率,列出分布列,代入期望的公式,即可求解数学期望.
试题解析:
(I)由以上统计数据填写下面 2×2 列联表,如下;
年龄不低于45岁的人 | 年龄低于45岁的人 | 合计 | |
赞成 | 10 | 27 | 37 |
不赞成 | 10 | 3 | 13 |
合计 | 20 | 30 | 50 |
根据公式计算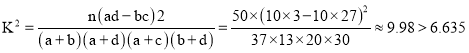 ,
,
所以有99%的把握认为年龄45岁为分界点对使用微信交流的态度有差异;
(Ⅱ)根据题意,X的所有可能取值为0,1,2,3,
则![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
随机变量X的分布列为:
| 0 | 1 | 2 | 3 |
P |
|
|
|
|
所以X的数学期望为![]()

练习册系列答案
相关题目