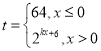题目内容
【题目】选修4﹣4:坐标系与参数方程
在平面直角坐标系x0y中,动点A的坐标为(2﹣3sinα,3cosα﹣2),其中α∈R.在极坐标系(以原点O为极点,以x轴非负半轴为极轴)中,直线C的方程为ρcos(θ﹣ ![]() )=a.
)=a.
(1)判断动点A的轨迹的形状;
(2)若直线C与动点A的轨迹有且仅有一个公共点,求实数a的值.
【答案】
(1)解:设动点A的直角坐标为(x,y),则 ![]() ,利用同角三角函数的基本关系消去参数α可得,
,利用同角三角函数的基本关系消去参数α可得,
(x﹣2)2+(y+2)2=9,点A的轨迹为半径等于3的圆.
(2)解:把直线C方程为ρcos(θ﹣ ![]() )=a化为直角坐标方程为
)=a化为直角坐标方程为 ![]() +
+ ![]() =2a,
=2a,
由题意可得直线C与圆相切,故有 ![]() =3,解得 a=3 或a=﹣3.
=3,解得 a=3 或a=﹣3.
【解析】(1)设动点A的直角坐标为(x,y),则 ![]() ,利用同角三角函数的基本关系消去参数α可得直角坐标方程,从而得到点A的轨迹.(2)把直线C方程为直角坐标方程,由题意可得直线C与圆相切,故有圆心到直线的距离等于半径,由此解得 a 的值.
,利用同角三角函数的基本关系消去参数α可得直角坐标方程,从而得到点A的轨迹.(2)把直线C方程为直角坐标方程,由题意可得直线C与圆相切,故有圆心到直线的距离等于半径,由此解得 a 的值.
【考点精析】解答此题的关键在于理解圆的参数方程的相关知识,掌握圆![]() 的参数方程可表示为
的参数方程可表示为![]() .
.

练习册系列答案
相关题目