题目内容
10.已知sinα+sinβ=$\frac{1}{2}$,tan$\frac{α+β}{2}$=2,求cosα+cosβ的值.分析 由tan$\frac{α+β}{2}$=2可得sin$\frac{α+β}{2}$=2cos$\frac{α+β}{2}$.再根据sinα+sinβ=$\frac{1}{2}$,利用和差化积与积化和差公式求得cosα+cosβ的值.
解答 解:由tan$\frac{α+β}{2}$=2,可得sin$\frac{α+β}{2}$=2cos$\frac{α+β}{2}$.
∵sinα+sinβ=2sin$\frac{α+β}{2}$cos$\frac{α-β}{2}$=4cos$\frac{α+β}{2}$•cos$\frac{α-β}{2}$=2(cosα+cosβ)=$\frac{1}{2}$,
∴cosα+cosβ=$\frac{1}{4}$.
点评 本题主要考查同角三角函数的基本关系,和差化积与积化和差公式的应用,属于基础题.

练习册系列答案
相关题目
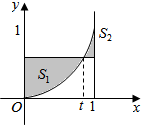 在区间[0,1]上给定曲线y=x2.
在区间[0,1]上给定曲线y=x2.