题目内容
已知平面向量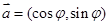 ,
, ,
, ,其中
,其中 ,且函数
,且函数 的图象过点
的图象过点 .
.
(1)求 的值;
的值;
(2)将函数 图象上各点的横坐标变为原来的的2倍,纵坐标不变,得到函数
图象上各点的横坐标变为原来的的2倍,纵坐标不变,得到函数 的图象,求函数
的图象,求函数 在
在 上的最大值和最小值.
上的最大值和最小值.
(1)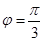 ;(2)最小值
;(2)最小值 ,最大值
,最大值 .
.
解析试题分析:(1)根据向量的数量积的坐标运算,求出 代入:
代入:
整理便得 ,再根据
,再根据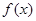 过点
过点 可得
可得 的值;
的值;
(2)将函数 图象上各点的横坐标变为原来的的2倍,纵坐标不变,便将函数
图象上各点的横坐标变为原来的的2倍,纵坐标不变,便将函数 中的
中的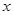 换成
换成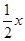 便得函数
便得函数 的解析式:
的解析式: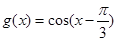 .
.
由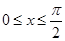 得
得 .
.
结合 的图象可得
的图象可得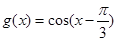 在
在 上的最大值和最小值.
上的最大值和最小值.
试题解析:(1) 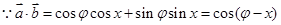 1分
1分 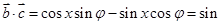
 2分
2分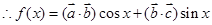
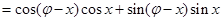
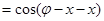
 , 4分
, 4分
即
∴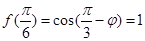 ,
,
而 ,
,
∴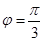 . 6分
. 6分
(2)由(1)得,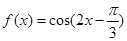 ,
,
于是 ,
,
即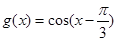 . 9分
. 9分
当 时,
时,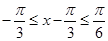 ,
,
所以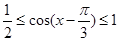 , 11分
, 11分
即当 时,
时, 取得最小值
取得最小值 ,
,
当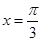 时,
时, 取得最大值
取得最大值 . 13分
. 13分
考点:1、向量的坐标运算;2、三角变换;3、三角函数的图象变换;4、三角函数的最值

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
试探究下列一组数列的基本规律:0,2,6,14,30,…,根据规律写出第6个符合规律的数,这个数是( )
| A.60 | B.62 | C.64 | D.94 |
[2013·江西抚州月考]数列{an}的前n项积为n2,那么当n≥2时,{an}的通项公式为( )
| A.an=2n-1 | B.an=n2 |
C.an= | D.an= |
若数列{an}满足 -
- =d(n∈N*,d为常数),则称数列{an}为“调和数列”.已知正项数列{
=d(n∈N*,d为常数),则称数列{an}为“调和数列”.已知正项数列{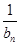 }为“调和数列”,且b1+b2+…+b9=90,则b4·b6的最大值是( )
}为“调和数列”,且b1+b2+…+b9=90,则b4·b6的最大值是( )
| A.10 | B.100 | C.200 | D.400 |
 是单位圆上一点,一个动点从点
是单位圆上一点,一个动点从点 出发,沿圆周按逆时针方向匀速旋转,12秒旋转一周.
出发,沿圆周按逆时针方向匀速旋转,12秒旋转一周. 秒时,动点到达点
秒时,动点到达点 ,
, 秒时动点到达点
秒时动点到达点 .设
.设 ,其纵坐标满足
,其纵坐标满足 .
.
 ;
; ,求
,求 的取值范围.
的取值范围. 中,角
中,角 的对边分别为
的对边分别为 向量
向量 ,
, ,且
,且 .
. 的值;
的值; ,
, ,求角
,求角 的大小及向量
的大小及向量 在
在 方向上的投影.
方向上的投影. 为抛物线
为抛物线 (
( )的焦点,
)的焦点,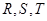 为该抛物线上三点,若
为该抛物线上三点,若 ,且
,且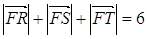
 的方程;
的方程; 点的坐标为(
点的坐标为(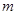 ,
, )其中
)其中 ,过点F作斜率为
,过点F作斜率为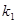 的直线与抛物线交于
的直线与抛物线交于 、
、 两点,
两点, 、
、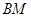 并延长交抛物线于
并延长交抛物线于 、
、 两点,设直线
两点,设直线 的斜率为
的斜率为 .若
.若 ,求
,求