题目内容
设 为抛物线
为抛物线 (
( )的焦点,
)的焦点,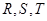 为该抛物线上三点,若
为该抛物线上三点,若 ,且
,且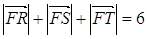
(Ⅰ)求抛物线 的方程;
的方程;
(Ⅱ) 点的坐标为(
点的坐标为(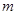 ,
, )其中
)其中 ,过点F作斜率为
,过点F作斜率为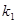 的直线与抛物线交于
的直线与抛物线交于 、
、 两点,
两点, 、
、 两点的横坐标均不为
两点的横坐标均不为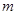 ,连结
,连结 、
、 并延长交抛物线于
并延长交抛物线于 、
、 两点,设直线
两点,设直线 的斜率为
的斜率为 .若
.若 ,求
,求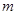 的值.
的值.
(Ⅰ)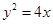 (Ⅱ)
(Ⅱ)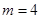 .
.
解析试题分析:(Ⅰ)利用向量和为0得到三点横坐标和的关系,结合三个向量的模为6得到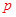 的值,求出抛物线的方程;(Ⅱ)通过点坐标表示斜率,设直线方程,联立直线方程与抛物线方程利用韦达定理得到关于
的值,求出抛物线的方程;(Ⅱ)通过点坐标表示斜率,设直线方程,联立直线方程与抛物线方程利用韦达定理得到关于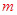 的方程,计算得到
的方程,计算得到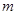 .
.
(Ⅰ)设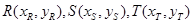
则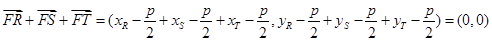 2分
2分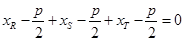 , 所以
, 所以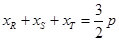 .
.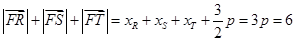 4分
4分
所以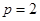 ,所以
,所以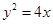 为所求. 5分
为所求. 5分
(Ⅱ)设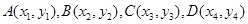
则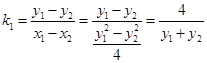 ,同理
,同理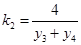 7分
7分
所以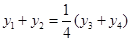
设AC所在直线方程为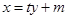 ,
,
联立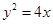 得,
得,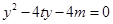 ,所以
,所以 , 9分
, 9分
同理 ,
,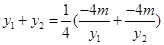 .
.
所以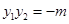 11分
11分
设AB所在直线方程为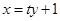 ,联立
,联立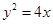 得,
得,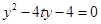 ,
,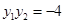
所以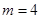 12分
12分
考点:抛物线标准方程,直线与抛物线联立,韦达定理应用.

数列 的通项公式为
的通项公式为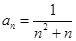 ,其前
,其前 项和为
项和为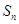 ,则
,则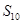 的值为 ( )
的值为 ( )
A.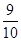 | B.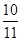 | C.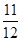 | D.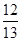 |
已知数列{an}的前n项和Sn=2n+1-2,等差数列{bn}中,b2=a2,且bn+3+bn-1=2bn+4,(n 2,n
2,n N+),则bn=
N+),则bn=
| A.2n+2 | B.2n | C.n-2 | D.2n-2 |
如图,第(1)个图案由1个点组成,第(2)个图案由3个点组成,第(3)个图案由7个点组成,第(4)个图案由13个点组成,第(5)个图案由21个点组成,……,依此类推,根据图案中点的排列规律,第100个图形由多少个点组成( )
| A.9900 | B.9901 | C.9902 | D.9903 |
在正项数列{an}中,若a1=1,且对所有n∈N*满足nan+1-(n+1)an=0,则a2014=( )
| A.1011 | B.1012 | C.2013 | D.2014 |
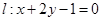 与⊙C:
与⊙C: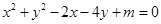 (
(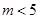 )
)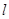 与⊙C相交,求
与⊙C相交,求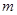 的取值范围。
的取值范围。 ,b=
,b= ,且x∈
,且x∈ .
. ,求正实数λ的值.
,求正实数λ的值. ,
, ,
, ,其中
,其中 为
为 的内角.
的内角. 的大小;
的大小; ,且
,且 ,求
,求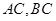 的长.
的长.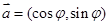 ,
, ,
, ,其中
,其中 ,且函数
,且函数 的图象过点
的图象过点 .
. 的值;
的值; 图象上各点的横坐标变为原来的的2倍,纵坐标不变,得到函数
图象上各点的横坐标变为原来的的2倍,纵坐标不变,得到函数 的图象,求函数
的图象,求函数 上的最大值和最小值.
上的最大值和最小值.