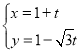题目内容
【题目】已知椭圆![]() :
:![]() ,
,![]() ,
,![]() 为椭圆
为椭圆![]() 的左、右顶点,椭圆的右焦点为
的左、右顶点,椭圆的右焦点为![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() .
.
(1)设直线![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点,且
两点,且![]() ,求
,求![]() 的值;
的值;
(2)设过点![]() 且斜率为1的直线与椭圆交于
且斜率为1的直线与椭圆交于![]() ,
,![]() (其中
(其中![]() ,
,![]() 分别在
分别在![]() 轴的上、下方)两点,当
轴的上、下方)两点,当![]() 时,记
时,记![]() 、
、![]() 的面积分别为
的面积分别为![]() 、
、![]() ,求
,求![]() 的最小值,并求此时椭圆的标准方程.
的最小值,并求此时椭圆的标准方程.
【答案】(1)![]()
(2)最小值为![]() ,此时椭圆的标准方程为
,此时椭圆的标准方程为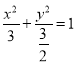
【解析】
(1)设![]() 在
在![]() 轴上方,根据
轴上方,根据![]() ,利用直角三角形中线定理得到
,利用直角三角形中线定理得到![]() ,,再由直线的倾斜角为
,,再由直线的倾斜角为![]() ,得到
,得到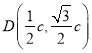 ,然后代入
,然后代入![]() 求解。
求解。
(2)设直线![]() 的方程为
的方程为![]() ,与
,与![]() 联立消去
联立消去![]() 得,
得,![]() ,利用三角形面积公式
,利用三角形面积公式![]() ,
,![]() ,结合韦达定理,建立
,结合韦达定理,建立![]() ,再利用基本不等式求最小值.
,再利用基本不等式求最小值.
(1)不妨设![]() 在
在![]() 轴上方.
轴上方.
因为直线![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点,所以
两点,所以![]() ,
,
因为椭圆的右焦点为![]() ,且
,且![]() ,所以
,所以![]() ,
,
设椭圆的半焦距为![]() ,则
,则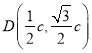 ,代入
,代入![]() 得,
得,![]() ,
,
因为![]() ,
,
所以![]() ,所以
,所以![]() ,
,
解得,![]() ;
;
(2)设直线![]() 的方程为
的方程为![]() (
(![]() 为椭圆的半焦距),
为椭圆的半焦距),
与![]() 联立消去
联立消去![]() 得,
得,![]() ,
,
设![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
![]()
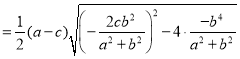
![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
同理得,![]() ,
,
所以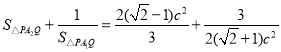
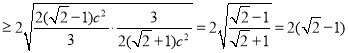 ,
,
当且仅当![]() ,即
,即![]() ,
,![]() ,
,![]() 时,取等号,
时,取等号,
所以![]() 取得最小值为
取得最小值为![]() ,
,
此时椭圆的标准方程为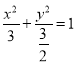 .
.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案【题目】某健身馆为响应十九届四中全会提出的“聚焦增强人民体质,健全促进全民健身制度性举措”,提高广大市民对全民健身运动的参与程度,推出了让健身馆会员参与的健身促销活动.
(1)为了解会员对促销活动的兴趣程度,现从某周六参加该健身馆健身活动的会员中随机采访男性会员和女性会员各![]() 人,他们对于此次健身馆健身促销活动感兴趣的程度如下表所示:
人,他们对于此次健身馆健身促销活动感兴趣的程度如下表所示:
感兴趣 | 无所谓 | 合计 | |
男性 |
|
|
|
女性 |
|
|
|
合计 |
|
|
|
根据以上数据能否有![]() 的把握认为“对健身促销活动感兴趣”与“性别”有关?
的把握认为“对健身促销活动感兴趣”与“性别”有关?
(参考公式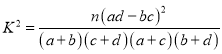 ,其中
,其中![]() )
)
|
|
|
|
|
|
|
|
|
|
|
|
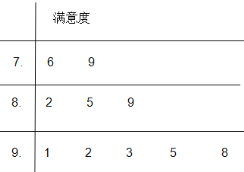
(2)在感兴趣的会员中随机抽取![]() 人对此次健身促销活动的满意度进行调查,以茎叶图记录了他们对此次健身促销活动满意度的分数(满分
人对此次健身促销活动的满意度进行调查,以茎叶图记录了他们对此次健身促销活动满意度的分数(满分![]() 分),如图所示,若将此茎叶图中满意度分为“很满意”(分数不低于
分),如图所示,若将此茎叶图中满意度分为“很满意”(分数不低于![]() 分)、“满意”(分数不低于平均分且低于
分)、“满意”(分数不低于平均分且低于![]() 分)、“基本满意”(分数低于平均分)三个级别.先从“满意”和“很满意”的会员中随机抽取两人参加回访馈赠活动,求这两人中至少有一人是“很满意”会员的概率.
分)、“基本满意”(分数低于平均分)三个级别.先从“满意”和“很满意”的会员中随机抽取两人参加回访馈赠活动,求这两人中至少有一人是“很满意”会员的概率.