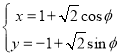题目内容
【题目】已知焦点在x轴上的椭圆C1的长轴长为8,短半轴为2![]() ,抛物线C2的顶点在原点且焦点为椭圆C1的右焦点.
,抛物线C2的顶点在原点且焦点为椭圆C1的右焦点.
(1)求抛物线C2的标准方程;
(2)过(1,0)的两条相互垂直的直线与抛物线C2有四个交点,求这四个点围成四边形的面积的最小值.
【答案】(1)y2=8x;(2)96.
【解析】
(1)由已知直接可求出椭圆的![]() ,运用椭圆
,运用椭圆![]() 之间的关系求出
之间的关系求出![]() ,最后可求出抛物线C2的标准方程;
,最后可求出抛物线C2的标准方程;
(2) 由题意易得两条直线的斜率存在且不为0,设其中一条直线l1的斜率为k,设出直线l1方程与抛物线方程联立,利用一元二次方程根与系数关系,可以求出弦长,同理求出直线l2与抛物线相交时,弦长的表达式,最后求出面积表达式,利用基本不等式可以求出四边形的面积的最小值.
(1)设椭圆半焦距为c(c>0),由题意得c![]() .
.
设抛物线C2的标准方程为y2=2px(p>0),则![]() ,∴p=4,
,∴p=4,
∴抛物线C2的标准方程为y2=8x;
(2)由题意易得两条直线的斜率存在且不为0,设其中一条直线l1的斜率为k,直线l1方程为y=k(x﹣1),则另一条直线l2的方程为y![]() (x﹣1),
(x﹣1),
联立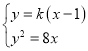 得k2x2﹣(2k2+8)x+k2=0,△=32k2+64>0,设直线l1与抛物线C2的交点为A,B,
得k2x2﹣(2k2+8)x+k2=0,△=32k2+64>0,设直线l1与抛物线C2的交点为A,B,
则则|AB|![]() |x2﹣x1|
|x2﹣x1|![]() ,
,
同理设直线l2与抛物线C2的交点为C,D,
则|CD|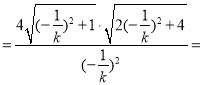 4
4![]() .
.
∴四边形的面积S![]() |AB||CD|
|AB||CD|![]() 4
4![]() .
.
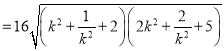 ,
,
令t![]() 2,则t≥4(当且仅当k=±1时等号成立),
2,则t≥4(当且仅当k=±1时等号成立),![]() .
.
∴当两直线的斜率分别为1和﹣1时,四边形的面积最小,最小值为96.

练习册系列答案
相关题目