题目内容
【题目】在四棱锥P–ABCD中,![]() ,
,![]() .
.
(1)设AC与BD相交于点M,![]() ,且
,且![]() 平面PCD,求实数m的值;
平面PCD,求实数m的值;
(2)若![]() ,
,![]() ,
,![]() ,且
,且![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.

【答案】(1)![]()
(2)![]()
【解析】
(1)由AB∥CD,得到![]() ,由MN∥平面PCD,得MN∥PC,从而
,由MN∥平面PCD,得MN∥PC,从而![]() ,由此能实数m的值;
,由此能实数m的值;
(2)由AB=AD,∠BAD=60°,知△ABD为等边三角形,推导出PD⊥DB,PD⊥AD,从而PD⊥平面ABCD,以D为坐标原点,![]() 的方向为x,y轴的正方向建立空间直角坐标系,由此能求出二面角B﹣PC﹣B的余弦值.
的方向为x,y轴的正方向建立空间直角坐标系,由此能求出二面角B﹣PC﹣B的余弦值.
解:(1)因为![]() ,所以
,所以![]() ,即
,即![]() .
.
因为![]() 平面PCD,
平面PCD,![]() 平面PAC,平面
平面PAC,平面![]() 平面
平面![]() ,
,
所以![]() .
.
所以![]() ,即
,即![]() .
.
(2)因为![]() ,
,![]() ,可知
,可知![]() 为等边三角形,
为等边三角形,
所以![]() ,又
,又![]() ,
,
故![]() ,所以
,所以![]() .
.
由已知![]() ,
,![]() ,所以
,所以![]() 平面ABCD,
平面ABCD,
如图,以D为坐标原点,![]() 的方向为x,y轴的正方向建立空间直角坐标系,
的方向为x,y轴的正方向建立空间直角坐标系,
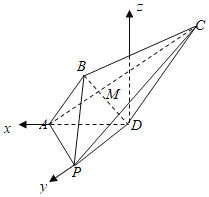
设![]() ,则
,则![]() ,
,![]() ,
,
所以![]() ,
,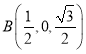 ,
,![]() ,
,![]() ,
,
则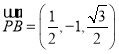 ,
,![]() ,
,![]()
设平面PBC的一个法向量为![]() ,则有
,则有
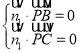 即
即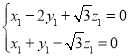 .
.
令![]() ,则
,则![]() ,即
,即![]() ,
,
设平面APC的一个法向量为![]() ,则有
,则有
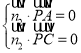 ,即
,即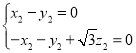
令![]() ,则
,则![]() ,即
,即![]() .
.
所以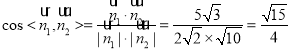
设二面角![]() 的平面角为
的平面角为![]() ,则
,则![]() .
.

练习册系列答案
相关题目