题目内容
【题目】已知函数![]() .
.
(1)若方程![]() 在
在![]() 内有两个不等实根,求
内有两个不等实根,求![]() 的取值范围(其中
的取值范围(其中![]() 为自然对数的底);
为自然对数的底);
(2)令![]() ,如果
,如果![]() 图象与
图象与![]() 轴交于
轴交于![]() ,
,![]()
![]() ,
,![]() 中点为
中点为![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() (2)证明见解析
(2)证明见解析
【解析】
(1)设![]() ,求
,求![]() ,令
,令![]() ,得到函数
,得到函数![]() 的单调区间,得出
的单调区间,得出![]() 的图像的大致走向,得出满足题意的不等式组,解得实数
的图像的大致走向,得出满足题意的不等式组,解得实数![]() 的取值范围.
的取值范围.
(2)由![]() ,
,![]() ,得
,得![]() ,将
,将![]() 坐标代入
坐标代入![]() ,再两式相减得
,再两式相减得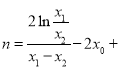 ,.然后假设
,.然后假设![]() ,代入消去参数
,代入消去参数![]() ,利用
,利用![]() 进行换元再构造函数
进行换元再构造函数![]() ,利用
,利用![]() 的单调性可得到与假设相矛盾的结论,从而证明结论.
的单调性可得到与假设相矛盾的结论,从而证明结论.
(1)设![]() ,则
,则![]()
由![]() 得
得![]() ,
,![]() 得
得![]() .
.
所以![]() 在
在![]() 单调递增,在
单调递增,在![]() 上单调递减.
上单调递减.
所以![]() 在
在![]() 单调递增,在
单调递增,在![]() 上单调递减.
上单调递减.
![]() ,
,![]() ,
,![]()
方程![]() 在
在![]() 内有两个不等实根
内有两个不等实根
所以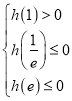 解得:
解得:![]() .
.
所以![]() 的取值范围是
的取值范围是![]()
(2)由![]() 为
为![]() 的中点有
的中点有![]() .
.
由点![]() ,
,![]()
![]() 在
在![]() 的图像上有.
的图像上有.
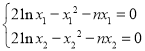 两式相减的
两式相减的![]()
即 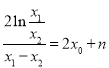 ,所以
,所以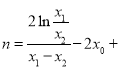
又![]() ,则
,则![]()
假设![]() 成立
成立
即![]() 成立.
成立.
则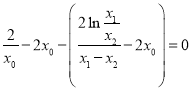 ,即
,即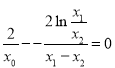
所以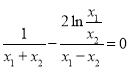 ,即
,即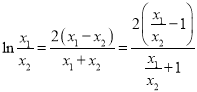
设![]() 由
由![]() 有
有![]()
设![]() ,则
,则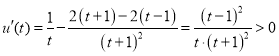
所以![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() .
.
则![]() ,即
,即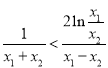 恒成立.
恒成立.
设与假设![]() 相矛盾.
相矛盾.
故假设不成立.
即![]() 成立.
成立.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
【题目】某企业为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取![]() 件产品作为样本称出它们的质量(单位:毫克),质量值落在
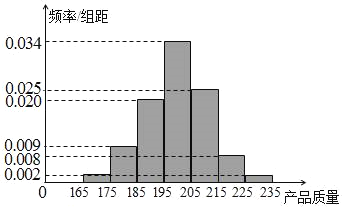
件产品作为样本称出它们的质量(单位:毫克),质量值落在![]() 的产品为合格品,否则为不合格品.如表是甲流水线样本频数分布表,如图是乙流水线样本的频率分布直方图.
的产品为合格品,否则为不合格品.如表是甲流水线样本频数分布表,如图是乙流水线样本的频率分布直方图.
产品质量/毫克 | 频数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(Ⅰ)以样本的频率作为概率,试估计从甲流水线上任取![]() 件产品,求其中不合格品的件数
件产品,求其中不合格品的件数![]() 的数学期望.
的数学期望.
甲流水线 | 乙流水线 | 总计 | |
合格品 | |||
不合格品 | |||
总计 |
(Ⅱ)由以上统计数据完成下面![]() 列联表,能否在犯错误的概率不超过
列联表,能否在犯错误的概率不超过![]() 的前提下认为产品的包装合格与两条自动包装流水线的选择有关?
的前提下认为产品的包装合格与两条自动包装流水线的选择有关?
(Ⅲ)由乙流水线的频率分布直方图可以认为乙流水线生产的产品质量![]() 服从正态分布
服从正态分布![]() ,求质量
,求质量![]() 落在
落在![]() 上的概率.
上的概率.
参考公式:![]()
![]()
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式:
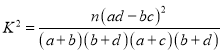 ,其中
,其中![]() .
.

