题目内容
【题目】已知P是曲线
上的点，Q是曲线
上的点，曲线
与曲线关于直线
对称，M为线段PQ的中点，O为坐标原点，则
的最小值为________．
【答案】
【解析】
画出函数
及其关于
对称的曲线的简图，根据图像，分别过P，Q作的平行线，如图虚线，由于中点在图中两条虚线的中间线上，要中点到原点的距离最小需要左边最近，右边最远，因此当两条虚线是如图所示曲线的切线时，此时切点分别是P，Q，此时P，Q的中点M到原点O的距离最小，利用相切求得切点坐标，即得解．
,
函数在
单调递增，
单调递减.
它的图像及关于直线对称的图像
如图所示：
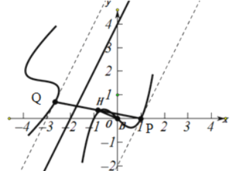
分别过P，Q作的平行线，如图虚线，由于中点在图中两条虚线的中间线上，要中点到原点的距离最小需要左边最近，右边最远，因此当两条虚线是如图所示曲线的切线时，此时切点分别是P，Q，此时P，Q的中点M到原点O的距离最小.
令
，又P在y轴右侧，
；
根据两条曲线的对称性，且P，Q处的切线斜率相等，点Q为点
关于对称的点，可求得
因此PQ中点坐标为：
故答案为：
练习册系列答案
相关题目
【题目】某种产品的质量以其质量指标值来衡量，质量指标值越大表明质量越好，记其质量指标值为
，当
时，产品为一级品；当
时，产品为二级品，当
时，产品为三级品，现用两种新配方（分别称为
配方和
配方）做实验，各生产了
件这种产品，并测量了每件产品的质量指标值，得到下面的试验结果 ：（以下均视频率为概率）
配方的频数分配表：
指标值分组 |
|
|
|
|
频数 |
|
|
|
|
配方的频数分配表：
指标值分组 |
|
|
|
|
|
频数 |
|
|
|
|
|
（1）若从配方产品中有放回地随机抽取
件，记“抽出的配方产品中至少
件二级品”为事件
，求事件发生的概率
；
（2）若两种新产品的利润率
与质量指标满足如下关系：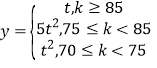
，其中
，从长期来看，投资哪种配方的产品平均利润率较大？
