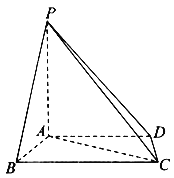
题目内容
【题目】已知椭圆
的左、右焦点分别为
，
是椭圆
上两点，
是坐标原点，且
，
，离心率为
.
（1）求椭圆的方程；
（2）过
作两条相互垂直的直线
分别交椭圆于
和
，求
的取值范围.
【答案】（1）
（2）[
].
【解析】
试题（1）根据椭圆几何性质以及定义得a，再根据离心率得c，解得b，（2）设直线方程，与椭圆方程联立，利用韦达定理以及弦长公式得
；再根据分式函数求值域，即得
的取值范围.
试题解析：（Ⅰ）连接
，由
知直线
过原点，根据椭圆的对称性知
，
由椭圆的定义知
，∴
，
由题知
，∴
，∴
，
故椭圆
的方程为
．
（Ⅱ）①当直线
有一条斜率不存在时，
．
②当
斜率存在且不为0时，设方程为
，
.
联立方程，得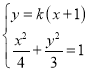
，消去
整理得
．
．
=
=
．
把
代入上式，得
，
，
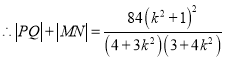设
，
，
，
设
=
，，
令
，则
，
=
（
），
∴
，∴
，
．
综上，的取值范围是[
].
练习册系列答案
相关题目
【题目】某高铁站停车场针对小型机动车收费标准如下：2小时内（含2小时）每辆每次收费5元；超过2小时不超过5小时，每增加一小时收费增加3元，不足一小时的按一小时计费；超过5小时至24小时内（含24小时）收费15元封顶。超过24小时，按前述标准重新计费.为了调查该停车场一天的收费情况，现统计1000辆车的停留时间（假设每辆车一天内在该停车场仅停车一次），得到下面的频数分布表：
T（小时） |
|
|
|
|
|
频数（车次） | 600 | 120 | 80 | 100 | 100 |
以车辆在停车场停留时间位于各区间的频率代替车辆在停车场停留时间位于各区间的概率。
（1）X表示某辆车在该停车场停车一次所交费用，求X的概率分布列及期望
；
（2）现随机抽取该停车场内停放的3辆车，
表示3辆车中停车费用少于的车辆数，求
的概率.
