Question

【题目】已知定点，圆，过R点的直线交圆于M，N两点过R点作直线交SM于Q点.

（1）求Q点的轨迹方程；

（2）若A，B为Q的轨迹与x轴的左右交点，为该轨迹上任一动点，设直线AP，BP分别交直线l：于点M，N，判断以MN为直径的圆是否过定点。如圆过定点，则求出该定点；如不是，说明理由.

Answer 1

【答案】(1) ;(2) 以MN为直径的圆经过定点

【解析】

(1) 利用,,可以推出,

根据可知: 动点的轨迹是以 为焦点,长轴长为4的椭圆,进而可以写出Q点的轨迹方程.

(2)设,求出的坐标后,再求出 的中点坐标,然后求出以 为直径的圆的方程,令可求得 为定值,所以圆过定点.

(1)如图:

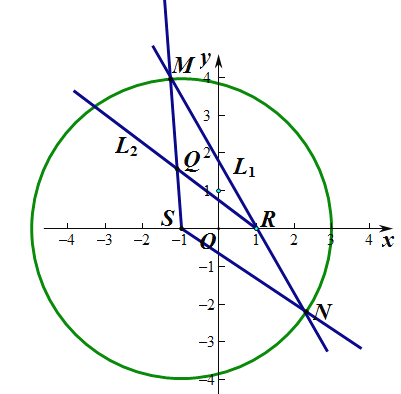
因为,,

所以,

所以,

根据椭圆的定义知:动点的轨迹是以 为焦点,长轴长为4的椭圆,

这里,

所以 点的轨迹方程为:.

(2)由题可知,设,

所以,则直线的方程为:,

令,则,

所以 ,

因为,则直线的方程为:,

令,则 ,所以,

所以的中点坐标为,此时圆的方程为:

,

令,得,又,所以 , 解得:,

故以MN为直径的圆经过定点.