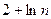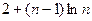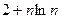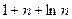题目内容
(本小题满分12分)
在数列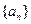 中,
中,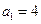 且对任意
且对任意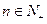 均有:
均有: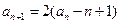
(I)证明数列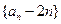 是等比数列;
是等比数列;
(II)求数列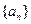 的通项公式;
的通项公式;
(Ⅲ)求证: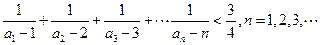
在数列
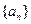 中,
中,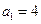 且对任意
且对任意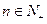 均有:
均有: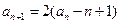
(I)证明数列
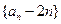 是等比数列;
是等比数列;(II)求数列
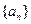 的通项公式;
的通项公式;(Ⅲ)求证:
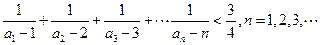
(I)由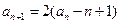 得:
得: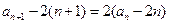 ,
,
所以数列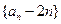 是等比数列。
是等比数列。
(II)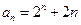 ,
,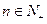
(Ⅲ)由于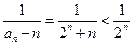
所以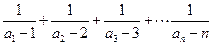
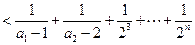
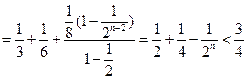 。
。
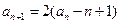 得:
得: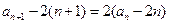 ,
,所以数列
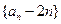 是等比数列。
是等比数列。(II)
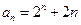 ,
,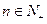
(Ⅲ)由于
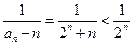
所以
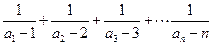
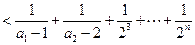
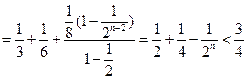 。
。解:(I)由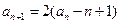 得:
得: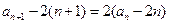 ,
,
所以数列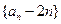 是等比数列。
是等比数列。
(II)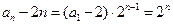 ,所以
,所以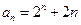 ,
,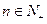 。
。
(Ⅲ)由于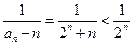
所以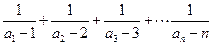
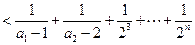
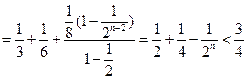 。
。
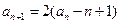 得:
得: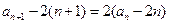 ,
,所以数列
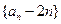 是等比数列。
是等比数列。(II)
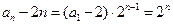 ,所以
,所以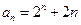 ,
,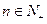 。
。(Ⅲ)由于
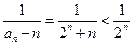
所以
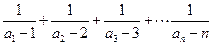
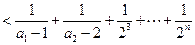
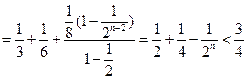 。
。
练习册系列答案
相关题目
 3分)
3分) 列
列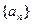 满足
满足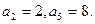
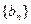 的前n项和为Tn若
的前n项和为Tn若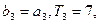 求Tn。
求Tn。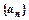 中,
中,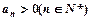 ,公比
,公比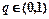 ,且
,且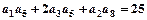 ,又
,又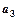 与
与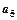 的等比中项为
的等比中项为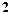 ,
,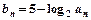 ,数列
,数列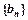 的前
的前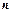 项和为
项和为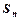 ,求数列
,求数列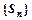 的通项公式
的通项公式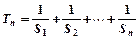 ,求
,求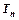
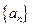 满足
满足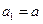 ,
,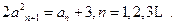
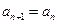 ,求
,求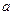 的值;
的值;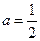 时,证明:
时,证明: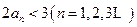 ;
;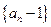 的前
的前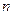 项之积为
项之积为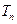 ,若对任意正整数
,若对任意正整数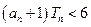 成立,求
成立,求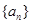 ,
,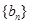 与函数
与函数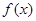 ,
,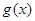 ,
,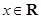 满足条件:
满足条件: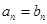 ,
,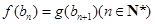 .
.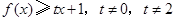 ,
,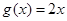 ,
,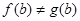 ,
,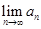 存在,求
存在,求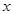 的取值范围;
的取值范围;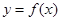 为
为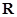 上的增函数,
上的增函数,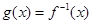 ,
,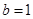 ,
,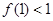 ,证明对任意
,证明对任意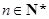 ,
,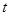 表示).
表示).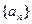 是首项
是首项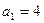 的等比数列,其前
的等比数列,其前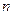 项和为Sn,且
项和为Sn,且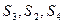 成等比数列.
成等比数列.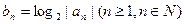 ,设
,设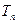 为数列
为数列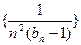 的前
的前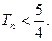
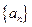 共有
共有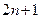 项,其中奇数项之和为319,偶数项
项,其中奇数项之和为319,偶数项 之和为290,则其中间项为 .
之和为290,则其中间项为 .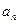 }中,
}中, ,则
,则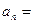 ( )
( )