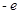题目内容
(本题满分15分)设函数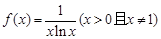 .
.
(Ⅰ)求函数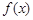 的单调区间;
的单调区间;
(Ⅱ)已知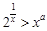 对任意
对任意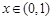 成立,求实数
成立,求实数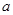 的取值范围;
的取值范围;
(Ⅲ)试讨论方程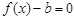 的零点个数.
的零点个数.
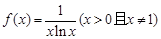 .
.(Ⅰ)求函数
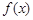 的单调区间;
的单调区间; (Ⅱ)已知
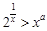 对任意
对任意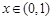 成立,求实数
成立,求实数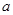 的取值范围;
的取值范围;(Ⅲ)试讨论方程
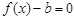 的零点个数.
的零点个数.(1)
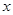 | 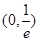 | 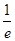 |  | 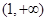 |
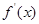 | + | 0 | - | - |
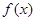 | 单调增 | 极大值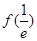 | 单调减 | 单调减 |
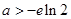
(3)b=-e或b>0时有一个零点;-e<b<=0时,有无零点;b<-e时,有两个零点.
本试题主要是考查了导数在研究函数中的运用。
(1)求单调区间既是求函数导数大于或小于0的区间,我们可以用图表表示使结果直观.
(2)对于未知数在指数上的式子,往往取对数进行解答.
(3)b=-e或b>0时有一个零点;-e<b<=0时,有无零点;b<-e时,有两个零点.
解 (1)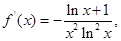 若
若 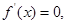 则
则 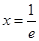 列表如下
列表如下
(2) 在 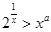 两边取对数, 得
两边取对数, 得 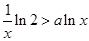 ,由于
,由于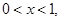 所以
所以
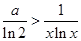 (1)
(1)
由(1)的结果可知,当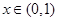 时,
时,  ,
,
为使(1)式对所有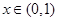 成立,当且仅当
成立,当且仅当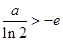 ,即
,即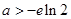
(Ⅲ)b=-e或b>0时有一个零点;-e<b<=0时,有无零点;b<-e时,有两个零点.
(1)求单调区间既是求函数导数大于或小于0的区间,我们可以用图表表示使结果直观.
(2)对于未知数在指数上的式子,往往取对数进行解答.
(3)b=-e或b>0时有一个零点;-e<b<=0时,有无零点;b<-e时,有两个零点.
解 (1)
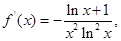 若
若 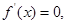 则
则 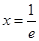 列表如下
列表如下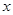 | 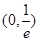 | 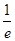 |  | 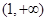 |
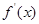 | + | 0 | - | - |
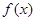 | 单调增 | 极大值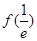 | 单调减 | 单调减 |
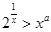 两边取对数, 得
两边取对数, 得 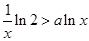 ,由于
,由于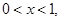 所以
所以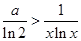 (1)
(1)由(1)的结果可知,当
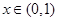 时,
时,  ,
, 为使(1)式对所有
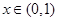 成立,当且仅当
成立,当且仅当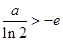 ,即
,即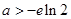
(Ⅲ)b=-e或b>0时有一个零点;-e<b<=0时,有无零点;b<-e时,有两个零点.

练习册系列答案
相关题目
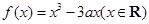 .
.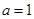 时,求
时,求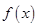 的极小值;
的极小值;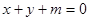 对任意的
对任意的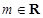 都不是曲线
都不是曲线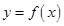 的切线,求
的切线,求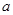 的取值范围.
的取值范围.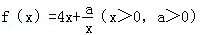 在x=3时取得最小值,则a= .
在x=3时取得最小值,则a= .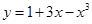 有( )
有( ) 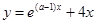 (
(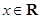 )有大于零的极值点,则实数
)有大于零的极值点,则实数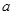 范围是 ( )
范围是 ( )



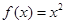 ,
, 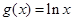 的图像分别交于点M,N,则当
的图像分别交于点M,N,则当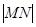 为最小时t的值为
为最小时t的值为


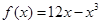 在区间
在区间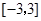 上的最小值是 .
上的最小值是 .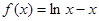 在区间
在区间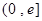 的最大值为( )
的最大值为( )