题目内容
已知定义在 上的奇函数
上的奇函数 ,当
,当 时,
时, ,那么,
,那么, .
.

【解析】
试题分析:因为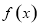 在
在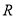 上为奇函数,所以
上为奇函数,所以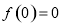 ;取
;取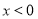 ,则
,则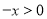 ,所以
,所以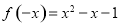 ,又因为
,又因为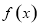 为奇函数,所以
为奇函数,所以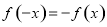 ,故
,故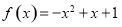 .综上得,
.综上得, .
.
考点:1.分段函数;2.函数的奇偶性.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
题目内容
已知定义在 上的奇函数
上的奇函数 ,当
,当 时,
时, ,那么,
,那么, .
.

【解析】
试题分析:因为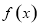 在
在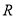 上为奇函数,所以
上为奇函数,所以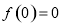 ;取
;取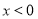 ,则
,则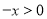 ,所以
,所以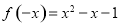 ,又因为
,又因为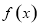 为奇函数,所以
为奇函数,所以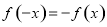 ,故
,故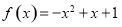 .综上得,
.综上得, .
.
考点:1.分段函数;2.函数的奇偶性.

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案