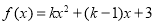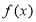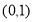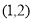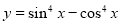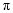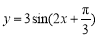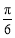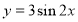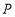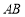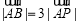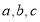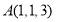题目内容
已知函数 (
(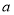 是常数且
是常数且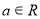 )
)
(1)若函数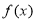 的一个零点是1,求
的一个零点是1,求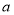 的值;
的值;
(2)求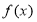 在
在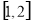 上的最小值
上的最小值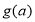 ;
;
(3)记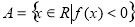 若
若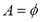 ,求实数
,求实数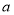 的取值范围。
的取值范围。
(1) ;(2)
;(2) ;(3)
;(3) .
.
【解析】
试题分析:(1)因为1是 的一个零点,将1代入得
的一个零点,将1代入得 ,求得
,求得 ;(2)由题意
;(2)由题意 ,先讨论二次项系数
,先讨论二次项系数 ,得最小值
,得最小值 ,然后讨论对称轴
,然后讨论对称轴 分别位于区间
分别位于区间 的各种情况,求出
的各种情况,求出 的最小值,合并得到
的最小值,合并得到 的最小值
的最小值 ,注意分类讨论时不重不漏;(3)由题意
,注意分类讨论时不重不漏;(3)由题意 即相当于
即相当于 恒成立,分离参数即可得
恒成立,分离参数即可得 恒成立,令
恒成立,令 ,
, ,分
,分 求得
求得 的最大值为
的最大值为 ,所以
,所以 .
.
试题解析:(1)由题意知 2分
2分
(2)
 ⅰ当
ⅰ当 时
时 3分
3分
ⅱ当 时,对称轴为
时,对称轴为
 4分
4分
ⅲ当 时,抛物线开口向下,对称轴
时,抛物线开口向下,对称轴
若 即
即 时,
时,
若 即
即 时,
时,
若 即
即 时,
时, 7分
7分
综上所述, 8分
8分
(3)由题意知:不等式 无解
无解
即 恒成立 10分
恒成立 10分
即 对任意
对任意 恒成立 11分
恒成立 11分
令 则
则 对任意
对任意 恒成立12分
恒成立12分
ⅰ当 时
时 13分
13分
ⅱ当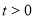 时
时 14分
14分
ⅲ当 时
时
 15分
15分
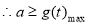 即
即 16分
16分
考点:1、函数的零点;2、二次函数在给定区间上的最值;3、分离参数处理恒成立问题;4、分类讨论思想.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目