题目内容
正方体ABCD-A1B1C1D1中,E为BC1的中点,则异面直线A1E与CD1所成角等于
| A.90° | B.60° | C.45° | D.30° |
D
解:连接A1B,BE,如图所示:
由正方体的几何特征可得A1B∥CD1,
故∠BA1E即为异面直线A1E与CD1所成角
设正方体ABCD-A1B1C1D1的棱长为2,
则在△A1BE中,A1B=2 ,BE=
,BE= ,A1E=
,A1E=
故cos∠BA1E=(A1B2+A1E 2-BE2) /(2A1B•A1E) =
故∠BA1E=30°
故选D
由正方体的几何特征可得A1B∥CD1,
故∠BA1E即为异面直线A1E与CD1所成角
设正方体ABCD-A1B1C1D1的棱长为2,
则在△A1BE中,A1B=2
 ,BE=
,BE= ,A1E=
,A1E=
故cos∠BA1E=(A1B2+A1E 2-BE2) /(2A1B•A1E) =

故∠BA1E=30°
故选D

练习册系列答案
相关题目
 中,
中, 侧面
侧面 ,已知
,已知


 ;(4分)
;(4分) 为
为 的中点时,求二面角
的中点时,求二面角 的平面角的正切值.(8分)
的平面角的正切值.(8分)
 底面ABCD,AB//DC,AD
底面ABCD,AB//DC,AD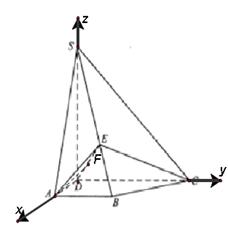
 的底面边长为2,高为4,则异面直线
的底面边长为2,高为4,则异面直线 与AD所成角的余弦值是________.
与AD所成角的余弦值是________. ,E为侧棱PC的中点,则PA与BE所成的角为( )
,E为侧棱PC的中点,则PA与BE所成的角为( )



 的侧棱长与底面边长都相等.点
的侧棱长与底面边长都相等.点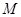 是线段
是线段 的中点,则直线
的中点,则直线 与侧面
与侧面 所成角的正切值等于 ( )
所成角的正切值等于 ( )



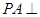 平面
平面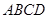 ,四边形
,四边形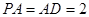 ,点
,点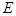 、
、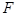 、
、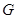 分别为线段
分别为线段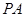 、
、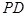 和
和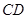 的中点.
的中点.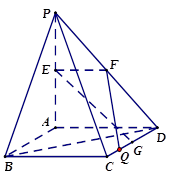
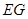 与
与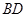 所成角的余弦值;
所成角的余弦值;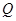 ,使得点
,使得点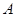 到平面
到平面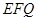 的距离恰为
的距离恰为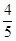 ?若存在,求出线段
?若存在,求出线段 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.