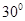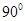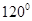题目内容
如图,四棱锥P-ABCD中,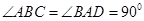 ,
,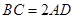 ,
,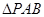 和
和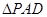 都是等边三角形.
都是等边三角形.

(Ⅰ)证明: ;
;
(Ⅱ)求二面角A-PD-C的大小.
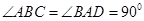 ,
,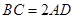 ,
,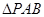 和
和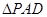 都是等边三角形.
都是等边三角形.
(Ⅰ)证明:
 ;
;(Ⅱ)求二面角A-PD-C的大小.
(Ⅰ)见解析(Ⅱ)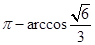
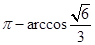
(Ⅰ)证明:取BC的中点E,连结DE,则ABED为正方形.
过P作PO⊥平面ABCD,垂足为O.
连结OA,OB,OD,OE.
由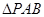 和
和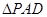 都是等边三角形知PA=PB=PD,
都是等边三角形知PA=PB=PD,
所以OA=OB=OD,即点O为正方形ABED对角线的交点,
故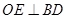 ,
,
从而 . 3分
. 3分
因为O是BD的中点,E是BC的中点,所以OE//CD.因此 . 5分
. 5分

(Ⅱ)解法一:
由(Ⅰ)知 ,
,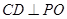 ,
, .
.
故 平面PBD.
平面PBD.
又 平面PBD,所以
平面PBD,所以 .
.
取PD的中点F,PC的中点G,连结FG,
则FG//CD,FG//PD.
连结AF,由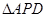 为等边三角形可得AF⊥PD.
为等边三角形可得AF⊥PD.
所以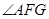 为二面角A-PD-C的平面角. 8分
为二面角A-PD-C的平面角. 8分
连结AG,EG,则EG//PB.
又PB⊥AE,所以EG⊥AE.
设AB=2,则 ,
,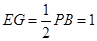 ,
,
故 .
.
在 中,
中, ,
, ,
, ,
,
所以 .
.
因此二面角A-PD-C的大小为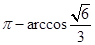 . 12分
. 12分
解法二:
由(Ⅰ)知,OE,OB,OP两两垂直.
以O为坐标原点,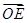 的方向为x轴的正方向建立如图所示的空间直角坐标系O-xyz.
的方向为x轴的正方向建立如图所示的空间直角坐标系O-xyz.

设 ,则
,则
 ,
, ,
, ,
, .
.
 ,
, .
.
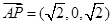 ,
, .
.
设平面PCD的法向量为 ,则
,则
 ,
,
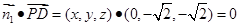 ,
,
可得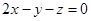 ,
, .
.
取 ,得
,得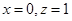 ,故
,故 . 8分
. 8分
设平面PAD的法向量为 ,则
,则
 ,
,
 ,
,
可得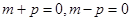 .
.
取m=1,得 ,故
,故 .
.
于是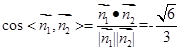 .
.
由于 等于二面角A-PD-C的平面角,
等于二面角A-PD-C的平面角,
所以二面角A-PD-C的大小为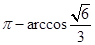 . 12分
. 12分
(1)解题的关键是辅助线的添加,取BC的中点E是入手点,然后借助三垂线定理进行证明;(2)利用三垂线定理法或者空间向量法求解二面角. 求二面角:关键是作出或找出其平面角,常用做法是利用三垂线定理定角法,先找到一个半平面的垂线,然后过垂足作二面角棱的垂线,再连接第三边,即可得到平面角。若考虑用向量来求:要求出二个面的法向量,然后转化为 ,要注意两个法向量的夹角与二面角可能相等也可能互补,要从图上判断一下二面角是锐二面角还是钝二面角,然后根据余弦值确定相等或互补即可。
,要注意两个法向量的夹角与二面角可能相等也可能互补,要从图上判断一下二面角是锐二面角还是钝二面角,然后根据余弦值确定相等或互补即可。
【考点定位】本题考查线线垂直的证明和二面角的求解,考查学生的空间想象能力和计算能力。
过P作PO⊥平面ABCD,垂足为O.
连结OA,OB,OD,OE.
由
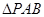 和
和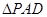 都是等边三角形知PA=PB=PD,
都是等边三角形知PA=PB=PD,所以OA=OB=OD,即点O为正方形ABED对角线的交点,
故
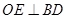 ,
,从而
 . 3分
. 3分因为O是BD的中点,E是BC的中点,所以OE//CD.因此
 . 5分
. 5分
(Ⅱ)解法一:
由(Ⅰ)知
 ,
,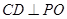 ,
, .
.故
 平面PBD.
平面PBD.又
 平面PBD,所以
平面PBD,所以 .
.取PD的中点F,PC的中点G,连结FG,
则FG//CD,FG//PD.
连结AF,由
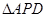 为等边三角形可得AF⊥PD.
为等边三角形可得AF⊥PD.所以
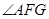 为二面角A-PD-C的平面角. 8分
为二面角A-PD-C的平面角. 8分连结AG,EG,则EG//PB.
又PB⊥AE,所以EG⊥AE.
设AB=2,则
 ,
,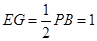 ,
,故
 .
.在
 中,
中, ,
, ,
, ,
,所以
 .
.因此二面角A-PD-C的大小为
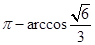 . 12分
. 12分解法二:
由(Ⅰ)知,OE,OB,OP两两垂直.
以O为坐标原点,
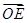 的方向为x轴的正方向建立如图所示的空间直角坐标系O-xyz.
的方向为x轴的正方向建立如图所示的空间直角坐标系O-xyz.
设
 ,则
,则 ,
, ,
, ,
, .
. ,
, .
.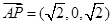 ,
, .
.设平面PCD的法向量为
 ,则
,则 ,
,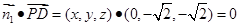 ,
,可得
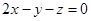 ,
, .
.取
 ,得
,得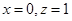 ,故
,故 . 8分
. 8分设平面PAD的法向量为
 ,则
,则 ,
, ,
,可得
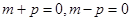 .
.取m=1,得
 ,故
,故 .
.于是
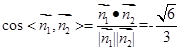 .
.由于
 等于二面角A-PD-C的平面角,
等于二面角A-PD-C的平面角,所以二面角A-PD-C的大小为
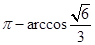 . 12分
. 12分(1)解题的关键是辅助线的添加,取BC的中点E是入手点,然后借助三垂线定理进行证明;(2)利用三垂线定理法或者空间向量法求解二面角. 求二面角:关键是作出或找出其平面角,常用做法是利用三垂线定理定角法,先找到一个半平面的垂线,然后过垂足作二面角棱的垂线,再连接第三边,即可得到平面角。若考虑用向量来求:要求出二个面的法向量,然后转化为
 ,要注意两个法向量的夹角与二面角可能相等也可能互补,要从图上判断一下二面角是锐二面角还是钝二面角,然后根据余弦值确定相等或互补即可。
,要注意两个法向量的夹角与二面角可能相等也可能互补,要从图上判断一下二面角是锐二面角还是钝二面角,然后根据余弦值确定相等或互补即可。【考点定位】本题考查线线垂直的证明和二面角的求解,考查学生的空间想象能力和计算能力。

练习册系列答案
相关题目
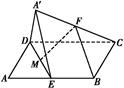
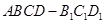 中,四边形
中,四边形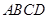 为菱形,
为菱形,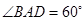 ,
,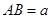 ,面
,面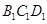 ∥面
∥面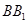 、
、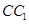 、
、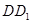 都垂直于面
都垂直于面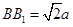 ,
,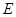 为
为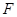 为
为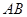 的中点.
的中点.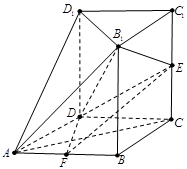
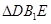 为等腰直角三角形;
为等腰直角三角形;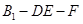 的大小.
的大小.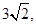 则AD和BC所成的角是( )
则AD和BC所成的角是( )
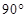
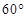
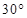
 是正方形,
是正方形,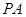 ⊥面
⊥面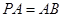 ,
,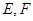 是侧棱
是侧棱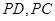 的中点.
的中点.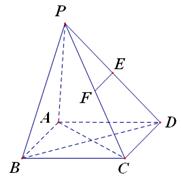
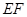 ∥平面
∥平面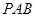 ;
;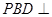 平面
平面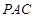 ;
; 与底面
与底面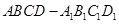 ,
,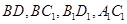 分别为各个面的对角线;
分别为各个面的对角线;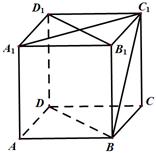
 ;
;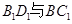 所成的角.
所成的角. 中,
中, 则
则 所成的角的大小是
所成的角的大小是



 中,
中, ,
, ,则异面直线
,则异面直线 与
与 所成的角为 ( )
所成的角为 ( )




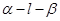 的大小为
的大小为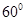 ,
,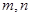 为异面直线,且
为异面直线,且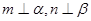 ,则
,则