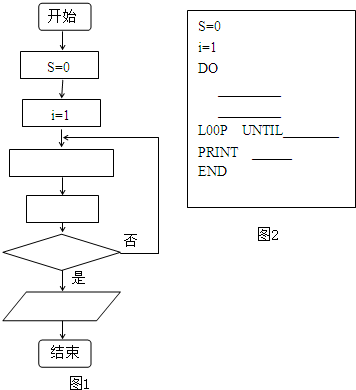
题目内容
12.设数列{an}的前n项和S由如下程序框图给出,若输入n的值为100,求输出的S.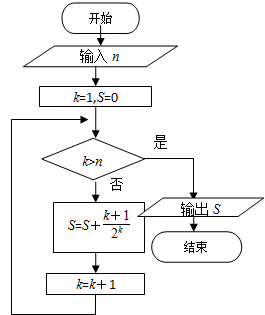
分析 由已知中的程序语句可知:该程序的功能是利用循环结构计算并输出变量S的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.
解答 解:由程序框图知:
S=$\frac{2}{{2}^{1}}+\frac{3}{{2}^{2}}+\frac{4}{{2}^{3}}+…+\frac{100}{{2}^{99}}+\frac{101}{{2}^{100}}$ ①
∴$\frac{1}{2}$S=$\frac{2}{{2}^{2}}+\frac{3}{{2}^{3}}+\frac{4}{{2}^{4}}+…+\frac{100}{{2}^{100}}+\frac{101}{{2}^{101}}$ ②
∴①-②得:$\frac{1}{2}$S=1+$\frac{1}{{2}^{1}}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+…+\frac{1}{{2}^{99}}+\frac{1}{{2}^{100}}-\frac{101}{{2}^{101}}$=$\frac{3}{2}$-$\frac{103}{{2}^{101}}$
∴S=3-$\frac{103}{{2}^{100}}$
点评 本题考查了程序框图的应用问题,解题时应模拟程序框图的运行过程,以便得出正确的结论,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.下列推理中属于类比推理的是( )
| A. | 一切偶数都能被2整除,2100是偶数,所以2100能被2整除. | |
| B. | 由a1,a2,a3…,归纳出数列的通项公式an | |
| C. | 由平面三角形的性质,推测空间四边形的性质 | |
| D. | 如果a>b,c>d,则a-d>b-c |
7.如图所示的程序框图,输出的S的值为( )
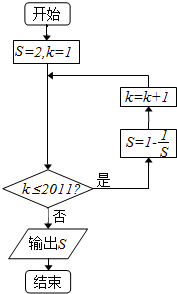

| A. | $\frac{1}{2}$ | B. | 2 | C. | -1 | D. | -$\frac{1}{2}$ |
1.演绎推理“因为指数函数y=ax(a>0,a≠1)是增函数,而函数y=0.5x是指数函数,所以y=0.5x是增函数”,所得结论错误的原因是( )
| A. | 大前提错误 | B. | 小前提错误 | ||
| C. | 推理形式错误 | D. | 大前提与小前提均错误 |
2.执行下面的程序框图,则输出的m的值为( )
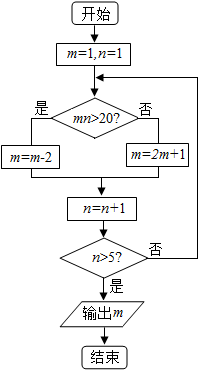

| A. | 9 | B. | 7 | C. | 5 | D. | 11 |