题目内容
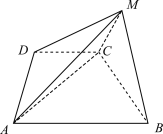
【题目】如图(1),在矩形![]() 中,
中,![]() ,
,![]() 在边
在边![]() 上,
上,![]() .沿
.沿![]() ,
,![]() 将
将![]() 和
和![]() 折起,使平面
折起,使平面![]() 和平面
和平面![]() 都与平面
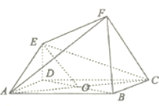
都与平面![]() 垂直,如图(2).
垂直,如图(2).
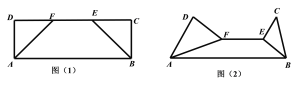
(1)试判断图(2)中直线![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)求平面![]() 和平面
和平面![]() 所成锐角二面角的余弦值.
所成锐角二面角的余弦值.
【答案】(1)![]() ∥
∥![]() .见解析(2)
.见解析(2)![]() .
.
【解析】
(1)分别取![]() ,
,![]() 的中点
的中点![]() ,
,![]() ,连结
,连结![]() ,
,![]() ,
,![]() ,
,![]() ,可证得
,可证得![]() 与
与![]() 都与平面
都与平面![]() 垂直,从而得它们平行且相等,得平行四边形
垂直,从而得它们平行且相等,得平行四边形![]() ,得
,得![]() ,在图(1)中可证得
,在图(1)中可证得![]() ,从而得结论;
,从而得结论;
(2)在![]() 边上取一点
边上取一点![]() ,使得
,使得![]() ,可证得
,可证得![]() ,
,![]() ,
,![]() 两两垂直.以
两两垂直.以![]() 点为坐标原点,直线
点为坐标原点,直线![]() ,
,![]() ,
,![]() 分别为坐标轴建立空间直角坐标系
分别为坐标轴建立空间直角坐标系![]() ,用空间向量法求二面角的余弦.
,用空间向量法求二面角的余弦.
解:(1)![]() .理由如下:
.理由如下:
连结![]() ,分别取
,分别取![]() ,
,![]() 的中点
的中点![]() ,
,![]() ,连结
,连结![]() ,
,![]() ,
,![]() ,由图(1)
,由图(1)
可得,![]() 与
与![]() 都是等腰直角三角形且全等,则
都是等腰直角三角形且全等,则![]() ,
,![]() ,
,![]() ,如图.
,如图.
∵平面![]() 平面
平面![]() ,交线为
,交线为![]() ,
,![]() 平面
平面![]() ,
,![]() ,∴
,∴![]() 平面
平面![]() .
.
同理得,![]() 平面
平面![]() ,∴
,∴![]() .
.
又∵![]() ∴四边形
∴四边形![]() 为平行四边形,∴
为平行四边形,∴![]() .
.
∵![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点∴
的中点∴![]()
∴![]() .
.
(2)在![]() 边上取一点
边上取一点![]() ,使得
,使得![]() .
.
由图(1)可得,![]() 为正方形,即
为正方形,即![]() .
.
∵![]() 为
为![]() 的中点∴
的中点∴![]() .
.
由(1)知,![]() 平面
平面![]() ,∴
,∴![]() ,
,![]() ,
,![]() 两两垂直.
两两垂直.
以![]() 点为坐标原点,直线
点为坐标原点,直线![]() ,
,![]() ,
,![]() 分别为坐标轴建立空间直角坐标系
分别为坐标轴建立空间直角坐标系![]() ,如图.
,如图.

设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() .
.
由 得
得![]() .
.
令![]() ,则
,则![]() ,
,![]() ,∴
,∴![]() .
.
由平面![]() 是坐标平面
是坐标平面![]() 可得:平面
可得:平面![]() 一个法向量为
一个法向量为![]() .
.
设平面![]() 与平面
与平面![]() 所成的锐角二面角为
所成的锐角二面角为![]() ,则
,则
 ,
,
∴平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() .
.

【题目】近年来,来自“一带一路”沿线的20国青年评选出了中国的“新四大发明”:高铁、扫码支付、共享单车和网购.其中共享单车既响应绿色出行号召,节能减排,保护环境,又方便人们短距离出行,增强灵活性.某城市试投放3个品牌的共享单车分别为红车、黄车、蓝车,三种车的计费标准均为每15分钟(不足15分钟按15分钟计)1元,按每日累计时长结算费用,例如某人某日共使用了24分钟,系统计时为30分钟.A同学统计了他1个月(按30天计)每天使用共享单车的时长如茎叶图所示,不考虑每月自然因素和社会因素的影响,用频率近似代替概率.设A同学每天消费![]() 元.
元.
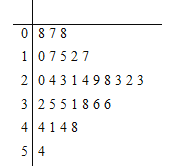
(1)求![]() 的分布列及数学期望;
的分布列及数学期望;
(2)各品牌为推广用户使用,推出APP注册会员的优惠活动:红车月功能使用费8元,每天消费打5折;黄车月功能使用费20元,每天前15分钟免费,之后消费打8折;蓝车月功能使用费45元,每月使用22小时之内免费,超出部分按每15分钟1元计费.设![]() 分别为红车,黄车,蓝车的月消费,写出
分别为红车,黄车,蓝车的月消费,写出![]() 与
与![]() 的函数关系式,参考(1)的结果,A同学下个月选择其中一个注册会员,他选哪个费用最低?
的函数关系式,参考(1)的结果,A同学下个月选择其中一个注册会员,他选哪个费用最低?
(3)该城市计划3个品牌的共享单车共3000辆正式投入使用,为节约居民开支,随机调查了100名用户一周的平均使用时长如下表:
时长 | (0,15] | (15,30] | (30,45] | (45,60] |
人数 | 16 | 45 | 34 | 5 |
在(2)的活动条件下,每个品牌各应该投放多少辆?