题目内容
【题目】对于定义域为
的函数
，如果存在区间
满足
是
上的单调函数，且在区间上的值域也为，则称函数为区间上的“保值函数”，为“保值区间”．根据此定义给出下列命题：①函数
是
上的“保值函数”；②若函数
是上的“保值函数”，则
；③对于函数
存在区间
，且
，使函数
为上的“保值函数”．其中所有真命题的序号为（ ）
A.②B.③C.①③D.②③
【答案】D
【解析】
①根据函数单调性定义和“保值函数”的概念判断即可，②结合函数
的图象可得结论，③由导数确定函数在
是单调递增的，而方程
有两个解
（
），构造新函数
，由零点存在定理确定
的零点
即可．
由“保值函数”定义可知
为区间
上的“保值函数”则在上是单调函数且在区间时其值域也为，那么当函数为增函数时满足条件
在上有两个不同的实数解
，
的函数就是“保值函数”，
命题①中
，虽满足在
上单调但值域为
，不是，故①为假命题；
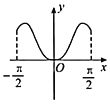
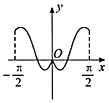
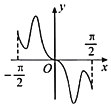
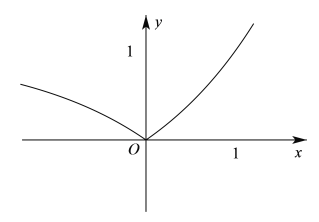
②中由
的图象可知，函数在上单调且值域为，其为区间上的“保值函数”故②为真命题；
③中
，则由
在
成立，所以
为上的增函数，再由解得有两个根
，，构造函数
，是减函数，
，
，由零点存在性定理知存在
，使成立，故③为真命题．综上所有真命题的序号为②③，
故选：D．
练习册系列答案
相关题目
