题目内容
【题目】函数f(x)=x2-(a+2)x+alnx(a∈R).
(1)求函数f(x)的单调区间;
(2)若a=4,y=f(x)的图象与直线y=m有三个交点,求m的取值范围.
【答案】(1)答案不唯一见解析(2)(4ln2-8,-5).
【解析】
(1)先求函数的定义域,再求函数的导数,分类讨论,确定![]() 与
与![]() 的关系,得到单调区间;
的关系,得到单调区间;
(2) 由a=4可根据(1) 中所确定函数的增减区间,求出函数的极小值和极大值即可得到答案.
(1)函数f(x)=x2-(a+2)x+alnx的定义域为(0,+∞),
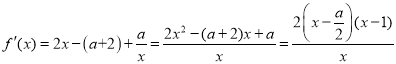
①当a≤0时,![]() )≤0在(0,1]上恒成立
)≤0在(0,1]上恒成立![]() ≥0在[1,+∞)上恒成立,
≥0在[1,+∞)上恒成立,
∴a≤0时,f(x)的增区间为[1,+∞),f(x)的减区间为(0,1].
②当0<a<2时,![]() ≥0在
≥0在![]() 和[1,+∞)上恒成立,
和[1,+∞)上恒成立,![]() ≤0在
≤0在
![]() 上恒成立.
上恒成立.
∴0<a<2时,f(x)的增区间为![]() 和[1,+∞),f(x)的减区间为
和[1,+∞),f(x)的减区间为![]()
③当a=2时,![]() ≥0在(0,+∞)上恒成立,
≥0在(0,+∞)上恒成立,
∴a=2时,f(x)的增区间为(0,+∞).
④当a>2时,![]() ≥0在(0,1]和
≥0在(0,1]和![]() 上恒成立,
上恒成立,
![]() ≤0在
≤0在![]() 上恒成立,
上恒成立,
∴a>2时,f(x)的增区间为(0,1]和![]() ,f(x)的减区间为
,f(x)的减区间为![]() .
.
(2)若a=4,由(1)可得f(x)在(0,1]上单调递增,在[1,2]上单调递减,在[2,+∞)上单调递增.
f(x)极小值=f(2)=4ln2-8,f(x)极大值=f(1)=-5,
∴y=f(x)的图象与直线y=m有三个交点时,m的取值范围是(4ln2-8,-5).

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案【题目】某市工业部门计划对所辖中小型企业推行节能降耗技术改造,下面是对所辖企业是否支持技术改造进行的问卷调查的结果:
支持 | 不支持 | 合计 | |
中型企业 | 40 | ||
小型企业 | 240 | ||
合计 | 560 |
已知从这560家企业中随机抽取1家,抽到支持技术改造的企业的概率为![]() .
.
(1)能否在犯错误的概率不超过0.025的前提下认为“是否支持节能降耗技术改造”与“企业规模”有关?
(2)从上述支持节能降耗的中小企业中按分层抽样的方法抽出12家企业,然后从这12家企业选出9家进行奖励,分别奖励中型企业50万元,小型企业10万元.设![]() 为所发奖励的金额.
为所发奖励的金额.
求![]() 的分布列和期望.
的分布列和期望.
附:![]()
| 0.05 | 0.025 | 0.01 |
| 3.841 | 5.024 | 6.635 |
【题目】下列说法中,错误的是( )
A.将一组数据中的每个数据都加上同一个常数后,方差不变
B.对于回归方程![]() ,变量
,变量![]() 每增加一个单位,
每增加一个单位,![]() 平均增加5个单位
平均增加5个单位
C.线性回归方程![]() 所对应的直线必过点
所对应的直线必过点![]()
D.在一个![]() 列联表中,由计算得
列联表中,由计算得![]() ,则有
,则有![]() 的把握说两个变量有关
的把握说两个变量有关
本题可以参考独立性检验临界值表
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
【题目】某校计划面向高二年级文科学生开设社会科学类和自然退坡在校本选修课程,某文科班有50名学生,对该班选课情况进行统计可知:女生占班级人数的60%,选社会科学类的人数占班级人数的70%,男生有10人选自然科学类.
(1)根据题意完成以下![]() 列联表:
列联表:
选择自然科学类 | 选择社会科学类 | 合计 | |
男生 | |||
女生 |
(2)判断是否有99%的把握认为科类的选择与性别有关?
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
附: ,其中
,其中![]() .
.