Question

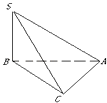
【题目】三棱锥S﹣ABC中，∠SBA=∠SCA=90°，△ABC是斜边AB=a的等腰直角三角形，则以下结论中： ①异面直线SB与AC所成的角为90°；
②直线SB⊥平面ABC；
③面SBC⊥面SAC；
④点C到平面SAB的距离是 ．

其中正确结论的序号是 ．

Answer 1

【答案】①②③④
【解析】解：由题意三棱锥S﹣ABC中，∠SBA=∠SCA=90°，知SB⊥BA，SC⊥CA， 又△ABC是斜边AB=a的等腰直角三角形可得AC⊥BC，又BC∩SB=B，故有AC⊥面SBC，故有SB⊥AC，故①正确，
由此可以得到SB⊥平面ABC，故②正确，
再有AC面SAC得面SBC⊥面SAC，故③正确，
△ABC是斜边AB=a的等腰直角三角形，点C到平面SAB的距离即点C到斜边AB的中点的距离，即 ，故④正确．
所以答案是①②③④
【考点精析】掌握异面直线及其所成的角和直线与平面垂直的判定是解答本题的根本，需要知道异面直线所成角的求法：1、平移法：在异面直线中的一条直线中选择一特殊点，作另一条的平行线；2、补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的在于容易发现两条异面直线间的关系；一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想．