题目内容
【题目】一条宽为![]() 的两平行河岸有村庄
的两平行河岸有村庄![]() 和供电站
和供电站![]() ,村庄
,村庄![]() 与
与![]() 的直线距离都是
的直线距离都是![]() ,
, ![]() 与河岸垂直,垂足为
与河岸垂直,垂足为![]() 现要修建电缆,从供电站
现要修建电缆,从供电站![]() 向村庄
向村庄![]() 供电.修建地下电缆、水下电缆的费用分别是
供电.修建地下电缆、水下电缆的费用分别是![]() 万元
万元![]() 、
、![]() 万元
万元![]() .
.
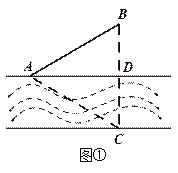
(1) 如图①,已知村庄![]() 与
与![]() 原来铺设有电缆
原来铺设有电缆![]() ,现先从
,现先从![]() 处修建最短水下电缆到达对岸后后,再修建地下电缆接入原电缆供电,试求该方案总施工费用的最小值;
处修建最短水下电缆到达对岸后后,再修建地下电缆接入原电缆供电,试求该方案总施工费用的最小值;
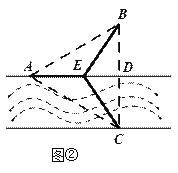
(2) 如图②,点![]() 在线段
在线段![]() 上,且铺设电缆的线路为
上,且铺设电缆的线路为![]() .若
.若![]() ,试用
,试用![]() 表示出总施工费用
表示出总施工费用![]() (万元)的解析式,并求
(万元)的解析式,并求![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)由已知可得![]() 为等边三角形,
为等边三角形, ![]() 水下电缆的最短线路为
水下电缆的最短线路为![]() ,过
,过![]() 作
作![]() 于
于![]() ,可知地下电缆的最短线路为
,可知地下电缆的最短线路为![]() ,由此能求出该方案的总费用;(2)因为
,由此能求出该方案的总费用;(2)因为![]() 所以
所以![]() .可得
.可得![]() ,利用导数研究函数的单调性,从而能求出施工总费用的最小值.
,利用导数研究函数的单调性,从而能求出施工总费用的最小值.
试题解析:(1)由已知可得![]() 为等边三角形.
为等边三角形.
因为![]() ,所以水下电缆的最短线路为
,所以水下电缆的最短线路为![]() .
.
过![]() 作
作![]() 于
于![]() ,可知地下电缆的最短线路为
,可知地下电缆的最短线路为![]() .
.
又![]() ,
,
故该方案的总费用为![]()
![]() (万元)
(万元)
(2)因为![]()
所以![]() .则
.则
![]() ,
,
令![]() 则
则

![]() ,
,
因为![]() ,所以
,所以![]() ,
,
记![]()
当![]() ,即
,即![]() 时,
时, ![]()
当![]() ,即
,即![]() 时,
时, ![]() ,
,
所以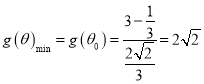 ,从而
,从而![]() ,
,
此时![]() ,
,
因此施工总费用的最小值为(![]() )万元,其中
)万元,其中![]() .
.

练习册系列答案
相关题目