题目内容
【题目】在极坐标系下，已知直线 
( 
)和圆 
.圆 
与直线 
的交点为 
.
（1）求圆 的直角坐标方程，并写出圆 的圆心与半径.
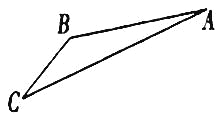
（2）求 
的面积.
【答案】
（1）解：∵ 
， 
，故 
，
∴圆 
的直角坐标方程为： 
.
∴圆 的标准方程为： 
，
∴圆 的圆心为 
，半径为1.
（2）解：将 
，代入 
，得： 
，解得： 
， 
.
故 
，即 
.
由于 的半径为1，所以 
的面积为 
.
【解析】对于 （1）要用到极坐标与直角坐标的互化公式，从而得到圆的直角坐标方程，化为标准方程，得到圆心坐标和半径.
对于（2）直线 l 1 : θ =
， ( ρ ∈ R )，表示的不是射线而是倾斜角为的直线，直接将直线的极坐标方程代入圆的极坐标方程中，可求出两交点A,B的极径，其差即为弦AB的长，在圆中由半径和弦长，可求出三角形的面积.
练习册系列答案
相关题目
【题目】假设关于某设备的使用年限x和支出的维修费用y（万元），有如下表的统计资料：
使用年限x | 2 | 3 | 4 | 5 | 6 |
维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料知y对x呈线性相关关系，试求：
（1）线性回归方程 
.
（2）估计使用年限为10年时，维修费用是多少.
（3）计算总偏差平方和、残差平方和及回归平方和.
（4）求 
并说明模型的拟合效果.
