题目内容
20．如图，已知向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$不共线，求作向量$\overrightarrow{a}$-$\overrightarrow{b}$-$\overrightarrow{c}$．
分析 根据向量的加法和减法的几何意义进行作图即可．
解答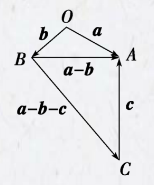 
解：如图：在平面内任意取一点0，作$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，
则$\overrightarrow{BA}$=$\overrightarrow{a}$-$\overrightarrow{b}$，
作$\overrightarrow{CA}$=$\overrightarrow{c}$，
则$\overrightarrow{BC}$=$\overrightarrow{a}$-$\overrightarrow{b}$-$\overrightarrow{c}$．
点评 本题主要考查向量作图，利用向量减法和加法的运算法则是解决本题的关键．
练习册系列答案
相关题目
10．若$\frac{sinθ-cosθ}{sinθ+cosθ}$=2，则sinθcosθ的值是（ ）
| A． | $\frac{3}{10}$ | B． | $\frac{3}{5}$ | C． | $\frac{1}{2}$ | D． | -$\frac{3}{10}$ |
8．已知函数f（x）=$\left\{\begin{array}{l}{lo{g}_{2}x-1，x≥1}\\{-{x}^{2}-ax，x＜1}\end{array}\right.$，f[f（1）]=1，则不等式x2+x-a＜0的解集为（ ）
| A． | （-2，1） | B． | （-1，$\frac{3}{2}$） | C． | （-$\frac{3}{2}$，1） | D． | （1，2） |
12．若实数x，y满足$\left\{\begin{array}{l}{（x-\sqrt{3}）^{2}+（y-1）^{2}≤1}\\{kx+y≥0}\\{kx-y≥0}\end{array}\right.$，点（x，y）表示的图形面积为π，则实数k的取值范围是（ ）
| A． | k≤-$\sqrt{3}$或k≥1 | B． | k≥1 | C． | k≤-$\sqrt{3}$或k$≥\sqrt{3}$ | D． | k≥$\sqrt{3}$ |
9．已知一次考试共有60名同学参加，考生的成绩X～N（110，52），据此估计，大约应有57人的分数在下列哪个区间内（ ）
| A． | （90，110] | B． | （95，125] | C． | （100，120] | D． | （105，115] |