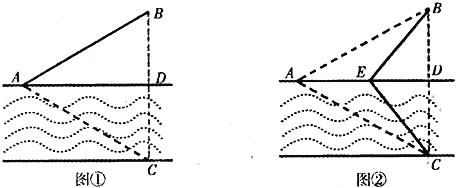
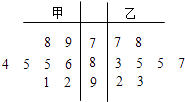
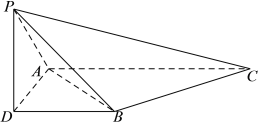
题目内容
【题目】已知函数f(x)=sin(ωx+)(ω>0)的部分图象如图所示,下面结论正确的个数是( )
①函数f(x)的最小正周期是2π
②函数f(x)的图象可由函数g(x)=sin2x的图象向左平移 ![]() 个单位长度得到
个单位长度得到
③函数f(x)的图象关于直线x= ![]() 对称
对称
④函数f(x)在区间[ ![]() ]上是增函数.
]上是增函数.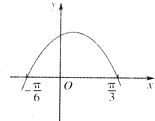
A.3
B.2
C.1
D.0
【答案】C
【解析】解:根据函数f(x)=sin(ωx+)(ω>0)的部分图象知, ![]() =
= ![]() ﹣(﹣
﹣(﹣ ![]() )=
)= ![]() ,
,
∴T=π,ω=2;
令2×(﹣ ![]() )+φ=0,解得φ=
)+φ=0,解得φ= ![]() ;
;
∴f(x)=sin(2x+ ![]() );
);
∴函数f(x)的最小正周期是π,①错误;
g(x)=sin2x的图象向左平移 ![]() 个单位长度,得到y=sin2(x+
个单位长度,得到y=sin2(x+ ![]() )=sin(2x+
)=sin(2x+ ![]() )的图象,不是f(x)的图象,②错误;
)的图象,不是f(x)的图象,②错误;
当x= ![]() 时,f(
时,f( ![]() )=sin(2×
)=sin(2× ![]() +
+ ![]() )=1,∴函数f(x)的图象关于直线x=
)=1,∴函数f(x)的图象关于直线x= ![]() 对称,③正确;
对称,③正确;
当x∈[ ![]() ]时,2x+
]时,2x+ ![]() ∈[
∈[ ![]() ,
, ![]() ],函数f(x)单调递减,④错误;
],函数f(x)单调递减,④错误;
综上,正确的命题是③.
故选:C.

【题目】几个月前,成都街头开始兴起“mobike”、“ofo”等共享单车,这样的共享单车为很多市民解决了最后一公里的出行难题.然而,这种模式也遇到了一些让人尴尬的问题,比如乱停乱放,或将共享单车占为“私有”等.
为此,某机构就是否支持发展共享单车随机调查了50人,他们年龄的分布及支持发展共享单车的人数统计如下表:
年龄 |
|
|
|
|
|
|
受访人数 | 5 | 6 | 15 | 9 | 10 | 5 |
支持发展 共享单车人数 | 4 | 5 | 12 | 9 | 7 | 3 |
(Ⅰ)由以上统计数据填写下面的![]() 列联表,并判断能否在犯错误的概率不超过0.1的前提下,认为年龄与是否支持发展共享单车有关系;
列联表,并判断能否在犯错误的概率不超过0.1的前提下,认为年龄与是否支持发展共享单车有关系;
年龄低于35岁 | 年龄不低于35岁 | 合计 | |
支持 | |||
不支持 | |||
合计 |
(Ⅱ)若对年龄在![]() ,
,![]() 的被调查人中各随机选取两人进行调查,记选中的4人中支持发展共享单车的人数为
的被调查人中各随机选取两人进行调查,记选中的4人中支持发展共享单车的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中
,其中![]() .
.