题目内容
【题目】定义域为集合![]() 上的函数
上的函数![]() 满足:①
满足:①![]() ;②
;②![]() (
(![]() );③
);③![]() 、
、![]() 、
、![]() 成等比数列;这样的不同函数
成等比数列;这样的不同函数![]() 的个数为________
的个数为________
【答案】![]()
【解析】
分析出f(x)的所有可能的取值,得到使f(x)中f(1)、f(6)、f(12)成等比数列时对应的项,再运用计数原理求出这样的不同函数f(x)的个数即可.
解:经分析,f(x)的取值的最大值为x,最小值为2﹣x,并且成以2为公差的等差数列,故f(6)的取值为6,4,2,0,﹣2,﹣4.
f(12)的取值为12,10,8,6,4,2,0,﹣2,﹣4,﹣6,﹣8,﹣10,
所以能使f(x)中的f(1)、f(6)、f(12)成等比数列时,f(1)、f(6)、f(12)的取值只有两种情况:
①f(1)=1、f(6)=2、f(12)=4;②f(1)=1、f(6)=﹣2、f(12)=4.
|f(x+1)﹣f(x)|=1(x=1,2,…,11),f(x+1)=f(x)+1,或者f(x+1)=f(x)﹣1,即得到后项时,把前项加1或者把前项减1.
(1)当f(1)=1、f(6)=2、f(12)=4时;将要构造满足条件的等比数列分为两步,第一步:从f(1)变化到f(6),第二步:从f(6)变化的f(12).
从f(1)变化到f(6)时有5次变化,函数值从1变化到2,故应从5次中选择3步加1,剩余的两次减1.对应的方法数为![]() 10种.
10种.
从f(6)变化到f(12)时有6次变化,函数值从2变化到4,故应从6次变化中选择4次增加1,剩余两次减少1,对应的方法数为![]() 15种.
15种.
根据分步乘法原理,共有10×15=150种方法.
(2)当f(1)=1、f(6)=﹣2、f(12)=4时,将要构造满足条件的等比数列分为两步,第一步:从f(1)变化到f(6),第二步:从f(6)变化的f(12).
从f(1)变化到f(6)时有5次变化,函数值从1变化到﹣2,故应从5次中选择1步加1,剩余的4次减1.对应的方法数为![]() 5种.
5种.
从f(6)变化到f(12)时有6次变化,函数值从﹣2变化到4,故应从6次变化中选择6次增加1,对应的方法数为![]() 1种.
1种.
根据分步乘法原理,共有5×1=5种方法.
综上,满足条件的f(x)共有:150+5=155种.
故填:155.

 名校课堂系列答案
名校课堂系列答案【题目】某创业者计划在某旅游景区附近租赁一套农房发展成特色“农家乐”,为了确定未来发展方向此创业者对该景区附近五家“农家乐”跟踪调查了100天,这五家“农家乐的收费标准互不相同得到的统计数据如下表,x为收费标准(单位:元/日),t为入住天数(单位:天),以频率作为各自的“入住率”,收费标准x与“入住率”y的散点图如图
x | 100 | 150 | 200 | 300 | 450 |
t | 90 | 65 | 45 | 30 | 20 |
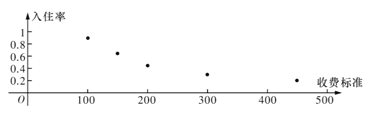
(1)若从以上五家“农家乐”中随机抽取两家深人调查,记![]() 为“入住率超过0.6的农家乐的个数,求
为“入住率超过0.6的农家乐的个数,求![]() 的概率分布列
的概率分布列
(2)z=lnx,由散点图判断![]() 与
与![]() 哪个更合适于此模型(给出判断即可不必说明理由)?并根据你的判断结果求回归方程(a,
哪个更合适于此模型(给出判断即可不必说明理由)?并根据你的判断结果求回归方程(a,![]() 的结果精确到0.1)
的结果精确到0.1)
(3)根据第(2)问所求的回归方程,试估计收费标准为多少时,100天销售额L最大?(100天销售额L=100×入住率×收费标准x)
参考数据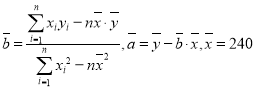 ,
,![]() ,
,![]()
![]()