题目内容
(本小题满分12分)已知函数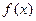 满足
满足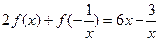 ,对任意
,对任意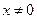 恒成立,在数列
恒成立,在数列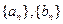 中,
中,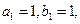 对任意
对任意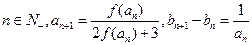
(1) 求函数的解析式
(2) 求数列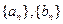 的通项公式
的通项公式
(3) 若对任意的实数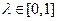 ,总存在自然数k,当
,总存在自然数k,当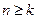 时,
时,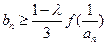 恒成立,求k的最小值。
恒成立,求k的最小值。
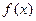 满足
满足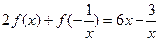 ,对任意
,对任意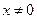 恒成立,在数列
恒成立,在数列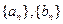 中,
中,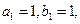 对任意
对任意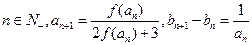
(1) 求函数的解析式
(2) 求数列
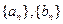 的通项公式
的通项公式(3) 若对任意的实数
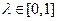 ,总存在自然数k,当
,总存在自然数k,当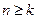 时,
时,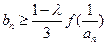 恒成立,求k的最小值。
恒成立,求k的最小值。解:(1)∵函数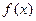
 满足
满足 …………①
…………①
 ……………………………………………②
……………………………………………②
由①②得 ………………………………………………3分
………………………………………………3分
(2) ,
,
即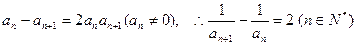
∴数列 是以
是以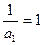 为首项,d = 2为公差的等差数列,
为首项,d = 2为公差的等差数列,
 ……………………………………………………………………6分
……………………………………………………………………6分



经检验得 也适合上式,
也适合上式,  ……………………9分
……………………9分
(3) 恒成立,
恒成立,
当 时,经验证符合题意;
时,经验证符合题意;
当 时,
时, 对任意实数
对任意实数 恒成立,
恒成立,
∴只须
 …………………………………………………………11分
…………………………………………………………11分
∴自然数k的最小值为3. …………………… 12分
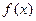
 满足
满足 …………①
…………① ……………………………………………②
……………………………………………②由①②得
 ………………………………………………3分
………………………………………………3分(2)
 ,
,即
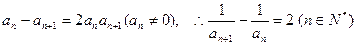
∴数列
 是以
是以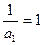 为首项,d = 2为公差的等差数列,
为首项,d = 2为公差的等差数列,
 ……………………………………………………………………6分
……………………………………………………………………6分


经检验得
 也适合上式,
也适合上式,  ……………………9分
……………………9分(3)
 恒成立,
恒成立,当
 时,经验证符合题意;
时,经验证符合题意;当
 时,
时, 对任意实数
对任意实数 恒成立,
恒成立,∴只须

 …………………………………………………………11分
…………………………………………………………11分∴自然数k的最小值为3. …………………… 12分
略

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
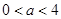 ,设函数
,设函数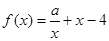 的两个不同的零点分别为
的两个不同的零点分别为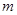 、
、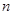 ,则
,则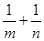 的取值范围是( )
的取值范围是( )



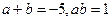 ,求
,求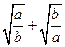 的值。
的值。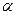 是方程
是方程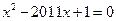 的一个根,试求
的一个根,试求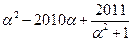 的值。
的值。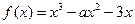
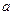 =2时,求
=2时,求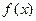 的零点;
的零点;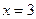 是
是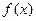 的极值点,求
的极值点,求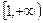 上是增函数,求实数
上是增函数,求实数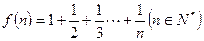 ,经计算得
,经计算得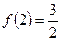 ,
,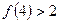 ,
,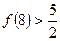 ,
,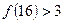 ,
,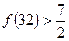 ,推测当
,推测当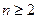 时,有
时,有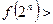 _____________。
_____________。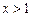 ,则
,则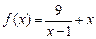 的最小值为 。
的最小值为 。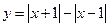 的最大值是
的最大值是 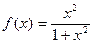 ,那么
,那么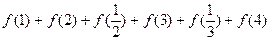
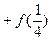 =______________
=______________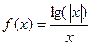 的图象可能是
的图象可能是