题目内容
【题目】已知函数![]() ,其中
,其中![]() .
.
(Ⅰ)函数![]() 的图象能否与
的图象能否与![]() 轴相切?若能,求出实数a,若不能,请说明理由;
轴相切?若能,求出实数a,若不能,请说明理由;
(Ⅱ)求最大的整数![]() ,使得对任意
,使得对任意![]() ,不等式
,不等式![]()
恒成立.
【答案】(1)不能(2)![]()
【解析】试题分析:
(Ⅰ)假设函数![]() 的图象能与
的图象能与![]() 轴相切.设切点为
轴相切.设切点为![]() ,根据导数的几何意义得到关于
,根据导数的几何意义得到关于![]() 的方程,然后判断此方程是否有解即可得到结论.(Ⅱ)将不等式变形为
的方程,然后判断此方程是否有解即可得到结论.(Ⅱ)将不等式变形为![]() ,设
,设![]() ,则问题等价于
,则问题等价于![]() 对任意
对任意![]() 恒成立,故只需函数
恒成立,故只需函数![]() 在R上单调递增,因此
在R上单调递增,因此![]() 在R上恒成立即可,由
在R上恒成立即可,由![]() 可得
可得
![]() ,即为
,即为![]() 成立的必要条件,然后再证
成立的必要条件,然后再证![]() 时,
时,![]() 即可得到结论.
即可得到结论.
试题解析:
(Ⅰ)∵![]() ,
,
∴![]() .
.
假设函数![]() 的图象与
的图象与![]() 轴相切于点
轴相切于点![]() ,
,
则有![]() , 即
, 即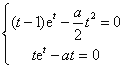 .
.
显然![]() ,将
,将![]() 代入方程
代入方程![]() 中可得
中可得![]() .
.
∵![]() ,
,
∴方程![]() 无解.
无解.
故无论a取何值,函数![]() 的图象都不能与
的图象都不能与![]() 轴相切.
轴相切.
(Ⅱ)由题意可得原不等式可化为![]() ,
,
故不等式![]() 在R上恒成立.
在R上恒成立.
设![]() ,则上式等价于
,则上式等价于![]() ,
,
要使![]() 对任意
对任意![]() 恒成立,
恒成立,
只需函数![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() 在
在![]() 上恒成立.
上恒成立.
则![]() ,解得
,解得![]() ,
,
∴![]() 在
在![]() 上恒成立的必要条件是:
上恒成立的必要条件是:![]() .
.
下面证明:当![]() 时,
时,![]() 恒成立.
恒成立.
设![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调递减;当
单调递减;当![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
∴![]() ,即
,即![]() .
.
则当![]() 时,
时,![]() ,
,![]() ;
;
当![]() 时,
时,![]() ,
,![]() .
.
∴![]() 恒成立.
恒成立.
所以实数![]() 的最大整数值为3.
的最大整数值为3.

练习册系列答案
相关题目
【题目】某老师对全班![]() 名学生学习积极性和参加社团活动情况进行调查,统计数据如下所示:
名学生学习积极性和参加社团活动情况进行调查,统计数据如下所示:
参加社团活动 | 不参加社团活动 | 合计 | |
学习积极性高 |
| ||
学习积极性一般 |
| ||
合计 |
|
|
(1)请把表格数据补充完整;
(2)若从不参加社团活动的![]() 人按照分层抽样的方法选取
人按照分层抽样的方法选取![]() 人,再从所选出的
人,再从所选出的![]() 人中随机选取两人作为代表发言,求至少有一个学习积极性高的概率;
人中随机选取两人作为代表发言,求至少有一个学习积极性高的概率;
(3)运用独立性检验的思想方法分析:请你判断是否有![]() 的把握认为学生的学习积极性与参与社团活动由关系?
的把握认为学生的学习积极性与参与社团活动由关系?
附: 
|
|
|
|
|
|
|
|