题目内容
.已知定义在R上的函数f(x)=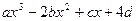 ( a , b , c , d∈R )的图象关于原点对称,且x = 1时,f(x)取极小值
( a , b , c , d∈R )的图象关于原点对称,且x = 1时,f(x)取极小值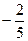 。
。
(Ⅰ)求f(x)的解析式;
(Ⅱ)当x∈[-1,1]时,图象旧否存在两点,使得此两面三刀点处的切线互相垂直?试证明你的结论;
(Ⅲ)若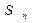 ∈[-1,1]时,求证:| f (
∈[-1,1]时,求证:| f (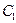 )-f(
)-f( )|≤
)|≤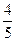 。
。
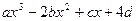 ( a , b , c , d∈R )的图象关于原点对称,且x = 1时,f(x)取极小值
( a , b , c , d∈R )的图象关于原点对称,且x = 1时,f(x)取极小值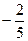 。
。(Ⅰ)求f(x)的解析式;
(Ⅱ)当x∈[-1,1]时,图象旧否存在两点,使得此两面三刀点处的切线互相垂直?试证明你的结论;
(Ⅲ)若
 ∈[-1,1]时,求证:| f (
∈[-1,1]时,求证:| f (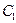 )-f(
)-f( )|≤
)|≤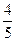 。
。(1)f(x)=
(2) 当x∈[-1,1]时,图象上不存在这样的两点使得结论成立
(3)同解析

(2) 当x∈[-1,1]时,图象上不存在这样的两点使得结论成立
(3)同解析
Ⅰ)∵函数f(x)的图象关于原点对称,
∴f(0)= 0,即4d = 0,∴d = 0
又f(-1)=" -" f(1),
即-a - 2b - c =" -a" + 2b – c ,∴b = 0
∴f(x)=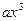 +cx ,f ′(x)= 3a
+cx ,f ′(x)= 3a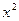 +c .
+c .
∵x = 1时,f(x)取极小值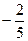 ,
,
∴ 3a + c = 0且 a + c =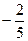 .
.
解得a =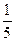 ,c =
,c = 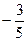 .
.
∴f(x)=
(Ⅱ)当x∈[-1,1]时,图象上不存在这样的两点使得结论成立。
假设图象上存在两点A(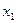 ,
,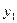 ),B(
),B( ,
,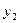 ),使得过此两点处的切线互相垂直,则由f ′(x)=
),使得过此两点处的切线互相垂直,则由f ′(x)=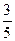 (
(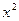 -1)知两点处的切线斜率分别为
-1)知两点处的切线斜率分别为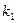 =
=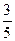
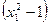 ,
,
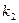 =
=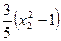 ,且
,且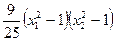 =" 1 " (*)
=" 1 " (*)
∵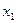 ,
, ∈[-1,1],
∈[-1,1],
∴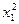 -1≤0,
-1≤0,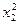 -1≤0
-1≤0
∴(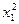 -1)(
-1)(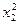 -1)≥0 此与(*)矛盾,故假设不成立
-1)≥0 此与(*)矛盾,故假设不成立
(Ⅲ)(理科)证明:f ′(x)=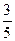 (
(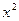 -1),令f ′(x)= 0,得x = ±1
-1),令f ′(x)= 0,得x = ±1
∴x∈(-∞,-1)或x∈(1,+∞)时,f ′(x)>0,x∈(-1,1)时,f ′(x)<0
∴f(x)在[-1,1]上是减函数,且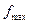 (x)=f(-1)=
(x)=f(-1)=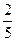 ,
, (x)=f(1)=
(x)=f(1)=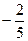 .
.
∴在[-1,1]上| f(x)|≤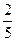 ,于是
,于是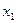 ,
, ∈[-1,1]时,
∈[-1,1]时,
|f(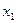 )-f(
)-f( )|≤|f(
)|≤|f(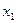 )|+|f(
)|+|f( )|≤
)|≤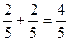
∴f(0)= 0,即4d = 0,∴d = 0
又f(-1)=" -" f(1),
即-a - 2b - c =" -a" + 2b – c ,∴b = 0
∴f(x)=
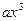 +cx ,f ′(x)= 3a
+cx ,f ′(x)= 3a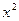 +c .
+c .∵x = 1时,f(x)取极小值
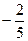 ,
,∴ 3a + c = 0且 a + c =
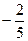 .
.解得a =
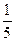 ,c =
,c = 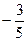 .
. ∴f(x)=

(Ⅱ)当x∈[-1,1]时,图象上不存在这样的两点使得结论成立。
假设图象上存在两点A(
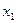 ,
,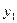 ),B(
),B( ,
,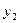 ),使得过此两点处的切线互相垂直,则由f ′(x)=
),使得过此两点处的切线互相垂直,则由f ′(x)=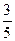 (
(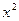 -1)知两点处的切线斜率分别为
-1)知两点处的切线斜率分别为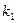 =
=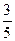
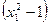 ,
,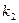 =
=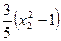 ,且
,且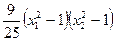 =" 1 " (*)
=" 1 " (*)∵
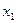 ,
, ∈[-1,1],
∈[-1,1],∴
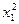 -1≤0,
-1≤0,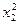 -1≤0
-1≤0∴(
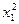 -1)(
-1)(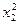 -1)≥0 此与(*)矛盾,故假设不成立
-1)≥0 此与(*)矛盾,故假设不成立 (Ⅲ)(理科)证明:f ′(x)=
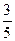 (
(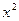 -1),令f ′(x)= 0,得x = ±1
-1),令f ′(x)= 0,得x = ±1∴x∈(-∞,-1)或x∈(1,+∞)时,f ′(x)>0,x∈(-1,1)时,f ′(x)<0
∴f(x)在[-1,1]上是减函数,且
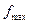 (x)=f(-1)=
(x)=f(-1)=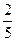 ,
, (x)=f(1)=
(x)=f(1)=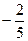 .
.∴在[-1,1]上| f(x)|≤
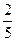 ,于是
,于是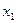 ,
, ∈[-1,1]时,
∈[-1,1]时,|f(
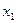 )-f(
)-f( )|≤|f(
)|≤|f(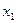 )|+|f(
)|+|f( )|≤
)|≤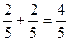

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
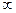 )上的函f(x)满足:(1)f(x)不恒为零;(2)对任何实数x、q,都有
)上的函f(x)满足:(1)f(x)不恒为零;(2)对任何实数x、q,都有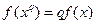 .
.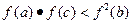 ;
;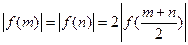 ,求证:
,求证: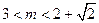
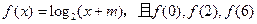 成等差数列.
成等差数列. 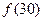 的值;
的值;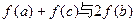 的大小关系,并证明你的结论.
的大小关系,并证明你的结论. 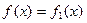 ,
,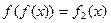 ,它们定义域的交集为
,它们定义域的交集为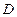 ,若对任意的
,若对任意的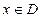 ,
,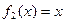 ,则称
,则称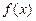 是集合
是集合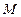 的元素.
的元素.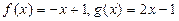 是否是
是否是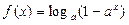 ,求
,求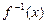 ,并判断
,并判断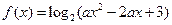
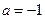 时,求该函数的定义域和值域;
时,求该函数的定义域和值域;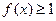 在区间
在区间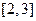 上恒成立,求实数
上恒成立,求实数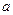 的取值范围.
的取值范围.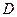 上的函数
上的函数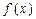 ,如果满足:对任意
,如果满足:对任意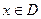 ,存在常数
,存在常数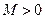 ,都有
,都有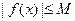 成立,则称
成立,则称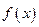 是
是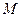 称为函数
称为函数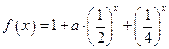 .
. 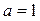 时,求函数
时,求函数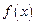 在
在 上的值域,并判断函数
上的值域,并判断函数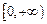 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数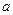 的取值范围.
的取值范围.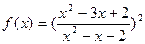 (其中
(其中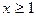 且
且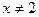 )
)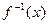
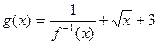 ,求函数g(x)最小值及相应的x值;
,求函数g(x)最小值及相应的x值;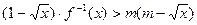 对于区间
对于区间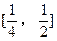 上的每一个x值都成立,求实数m的取值范围。
上的每一个x值都成立,求实数m的取值范围。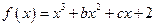 在
在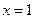 处取得极值
处取得极值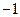 .
.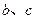 的值;
的值; 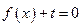 在区间
在区间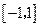 上有实根,求实数的取值范围.
上有实根,求实数的取值范围.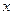 元/千克,政府补贴为
元/千克,政府补贴为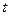 元/千克.根据市场调查,当
元/千克.根据市场调查,当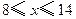 时,淡水鱼的市场日供产量
时,淡水鱼的市场日供产量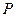 千克与市场日需求量
千克与市场日需求量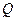 千克近似地满足关系:
千克近似地满足关系: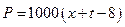 ,
,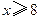 ,
,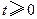 ,
,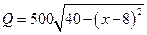 ,
,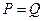 时的市场价格称为市场平衡价格.
时的市场价格称为市场平衡价格.