题目内容

11．若复数z=（x+i）（1+i）是纯虚数，其中x为实数，i为虚数单位，则z的共轭复数$\overline z$=-2i．

分析 利用复数代数形式的乘法运算展开并整理，由复数为纯虚数求得x值，则z可求，$\overline{z}$可求．

解答 解：由z=（x+i）（1+i）=（x-1）+（x+1）i是纯虚数，
得$\left\{\begin{array}{l}{x-1=0}\\{x+1≠0}\end{array}\right.$，即x=1，
∴z=2i，则$\overline{z}=-2i$．
故答案为：-2i．

点评 本题考查了复数代数形式的乘除运算，考查了复数为纯虚数的条件，是基础题．

练习册系列答案
相关题目
1．已知圆C：（x-1）2+（y-2）2=25，直线l：（2m+1）x+（m+1）y-7m-4=0．
（Ⅰ）求证：直线l与圆C必相交；
（Ⅱ）求直线l被圆C截得的弦长最短时直线l的方程以及最短弦长．
2．已知不共线向量$\overrightarrow{a}$，$\overrightarrow{b}$，|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|，则$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$的夹角是（　　）
A．$\frac{π}{2}$B．$\frac{π}{3}$C．$\frac{π}{4}$D．$\frac{π}{6}$
19．以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ=4cosθ，直线l的参数方程为$\left\{{\begin{array}{l}{x=t+a}\\{y=-\frac{{\sqrt{2}}}{2}t}\end{array}}\right.$（t为参数），则直线l将曲线C的周长分为1：5，则实数a=-1或5．
6．已知函数f（x）=sin4x．
（1）记g（x）=f（x）+f（$\frac{π}{2}$-x），求g（x）在[$\frac{π}{6}，\frac{3π}{8}$]上的最大值与最小值；
（2）求f（$\frac{π}{180}$）+f（$\frac{2π}{180}$）+f（$\frac{3π}{180}$）+…f（$\frac{88π}{180}$）+f（$\frac{89π}{180}$）的值．
16．若函数f（x）=2x-（k2-3）•2-x，则k=2是函数f（x）为奇函数的充分不必要条件．（选填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”）
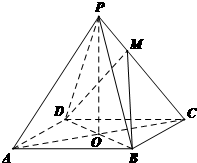3．如图，已知四棱锥P-ABCD的底面是菱形，对角线AC，BD交于点O，OA=4，OB=3，OP=4，OP⊥底面ABCD，设点M满足$\overrightarrow{PM}$=λ$\overrightarrow{MC}$（λ＞0）．
（1）当λ=$\frac{1}{2}$时，求直线PA与平面BDM所成角的正弦值；
（2）若二面角M-AB-C的大小为$\frac{π}{4}$，求λ的值．
20．已知一组函数fn（x）=sinnx+cosnx，x∈[0，$\frac{π}{2}$]，n∈N*，则下列说法正确的个数是（　　）
①?n∈N*，fn（x）≤$\sqrt{2}$恒成立
②若fn（x）为常数函数，则n=2
③f4（x）在[0，$\frac{π}{4}$]上单调递减，在[$\frac{π}{4}$，$\frac{π}{2}$]上单调递增．
A．0B．1C．2D．3
1．在区间[-2，4]上随机取一个点x，若x满足x2≤m的概率为$\frac{1}{4}$，则m=$\frac{9}{16}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网