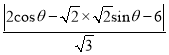题目内容
【题目】已知椭圆E:![]() =1(a>b>0)的两个焦点与短轴的一个端点是直角三角形的三个顶点,直线l:y=-x+3与椭圆E有且只有一个公共点T.
=1(a>b>0)的两个焦点与短轴的一个端点是直角三角形的三个顶点,直线l:y=-x+3与椭圆E有且只有一个公共点T.
(1)求椭圆E的方程及点T的坐标;
(2)设O是坐标原点,直线l'平行于OT,与椭圆E交于不同的两点A,B,且与直线l交于点P,证明:存在常数λ,使得|PT|2=λ|PA|·|PB|,并求λ的值.
【答案】(1)![]() =1,点T的坐标为(2,1);(2)存在常数λ=
=1,点T的坐标为(2,1);(2)存在常数λ=![]() ,使得|PT|2=λ|PA|·|PB|.
,使得|PT|2=λ|PA|·|PB|.
【解析】试题分析:
(1)由题意得椭圆E中a=![]() b,故椭圆E的方程为
b,故椭圆E的方程为![]() =1.把y=-x+3与椭圆E的方程联立消元后得到二次方程,由直线与椭圆有且只有一个公共点得到方程的判别式为0,可得b2=3,且得到方程的解为x=2,进而得到点T的坐标.(2)设直线l'的方程为y=
=1.把y=-x+3与椭圆E的方程联立消元后得到二次方程,由直线与椭圆有且只有一个公共点得到方程的判别式为0,可得b2=3,且得到方程的解为x=2,进而得到点T的坐标.(2)设直线l'的方程为y=![]() x+m,并求出直线l'与直线l的交点P
x+m,并求出直线l'与直线l的交点P![]() ,可得
,可得![]() ;再根据直线l'与椭圆的方程可得|PA|=
;再根据直线l'与椭圆的方程可得|PA|=![]() ,|PB|=
,|PB|=![]() ,计算可得|PA|·|PB|=
,计算可得|PA|·|PB|=![]() m2,比较可得存在常数λ=
m2,比较可得存在常数λ=![]() ,使得|PT|2=λ|PA|·|PB|.
,使得|PT|2=λ|PA|·|PB|.
试题解析:
(1)∵椭圆E的两个焦点与短轴的一个端点是直角三角形的三个顶点,
∴a=![]() b,
b,
∴椭圆E的方程为![]() =1.
=1.
由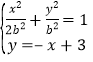 消去y整理得3x2
消去y整理得3x2![]() 12x+(18
12x+(18![]() 2b2)=0. ①
2b2)=0. ①
方程①的判别式为Δ=24(b2![]() 3),
3),
由Δ=0,得b2=3,
此时方程①的解为x=2,
∴椭圆E的方程为![]() =1,点T的坐标为(2,1).
=1,点T的坐标为(2,1).
(2)由已知可设直线l'的方程为y=![]() x+m(m≠0),
x+m(m≠0),
由方程组![]() 可得
可得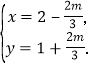
∴点P的坐标为![]() ,
,
∴![]() .
.
由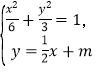 消去y整理得3x2+4mx+(4m2
消去y整理得3x2+4mx+(4m2![]() 12)=0. ②
12)=0. ②
方程②的判别式为Δ=16(9![]() 2m2).
2m2).
由Δ>0,得![]() <m<
<m<![]() .
.
设点A,B的坐标分别为A(x1,y1),B(x2,y2).
则x1+x2=![]() ,x1x2=
,x1x2=![]() .
.
∴|PA|=![]() =
=![]() ,
,
同理|PB|=![]() .
.
∴|PA|·|PB|=![]() =
=![]()
![]() =
=![]() m2.
m2.
由|PT|2=λ|PA|·|PB|可得λ=![]() .
.
∴存在常数λ=![]() ,使得|PT|2=λ|PA|·|PB|.
,使得|PT|2=λ|PA|·|PB|.