题目内容
已知函数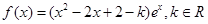 。
。
(1)求 的单调区间;
的单调区间;
(2)若 在区间
在区间 上的最小值为e,求k的值。
上的最小值为e,求k的值。
(1)当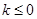 时,
时,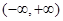 是函数
是函数 的单调增区间;当
的单调增区间;当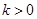 时,
时,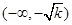 和
和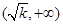 是函数
是函数 的单调递减区间,
的单调递减区间,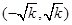 是函数
是函数 的单调递减区间。(2)
的单调递减区间。(2)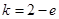 ;
;
解析试题分析:(1)求单调区间要求导数,令导函数大于0得增区间,导函数小于0得减区间,对于含参数的要对参数进行讨论,本题求导函数得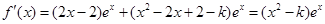 中要把
中要把 分
分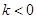 、
、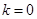 、
、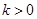 三种情况进行讨论;(2)利用(1)问中求得的单调区间求最值,在求最值的时候要对
三种情况进行讨论;(2)利用(1)问中求得的单调区间求最值,在求最值的时候要对 的范围进一步的讨论,在区间
的范围进一步的讨论,在区间 进行分类讨论。
进行分类讨论。
试题解析:解:(1)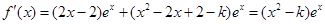 。 3分
。 3分
当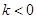 时,
时,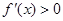 ,函数
,函数 在R上是增函数。
在R上是增函数。
当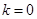 时,在区间
时,在区间 和
和 上
上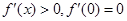 ,函数
,函数 在R上是增函数。 5分
在R上是增函数。 5分
当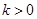 时,解
时,解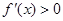 ,得
,得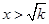 ,或
,或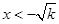 。解
。解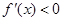 ,得
,得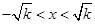 。
。
所以函数 在区间
在区间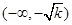 和
和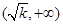 上是增函数,在区间
上是增函数,在区间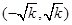 上是减函数。
上是减函数。
综上,当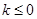 时,
时,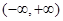 是函数
是函数 的单调增区间;当
的单调增区间;当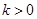 时,
时,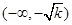 和
和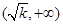 是函数
是函数 的单调递减区间,
的单调递减区间,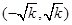 是函数
是函数 的单调递减区间。7分
的单调递减区间。7分
(2)当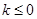 时,函数
时,函数 在R上是增函数,
在R上是增函数,
所以 在区间
在区间 上的最小值为
上的最小值为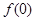 ,
,
依题意,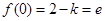 ,解得
,解得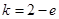 ,符合题意。 8分
,符合题意。 8分
当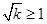 ,即
,即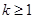 时,函数
时,函数 在区间
在区间 上是减函数。
上是减函数。
所以 在区间
在区间 上的最小值为
上的最小值为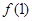 ,
,
解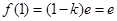 ,得
,得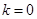 ,不符合题意。 9分
,不符合题意。 9分
当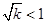 ,即
,即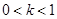 时,函数
时,函数 在区间
在区间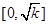 上是减函数,在区间
上是减函数,在区间
练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案
相关题目
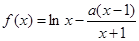 (
(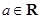 ,
,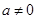 ),
),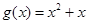 .
.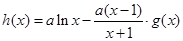 的单调区间,并确定其零点个数;
的单调区间,并确定其零点个数; 的取值范围;
的取值范围; (
( ).
).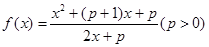 和
和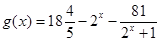 的定义域都是[2,4].
的定义域都是[2,4].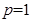 ,求
,求 的最小值;
的最小值;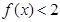 在其定义域上有解,求
在其定义域上有解,求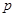 的取值范围;
的取值范围;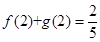 ,求证
,求证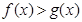 .
. 的定义域为
的定义域为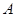 ,
,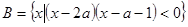 .
.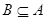 ,求实数
,求实数 的取值范围.
的取值范围. 是
是 上的增函数,
上的增函数,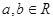 ,且
,且 ,求证
,求证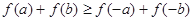
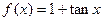 ,若
,若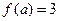 ,则
,则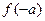 = .
= .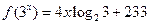 ,则
,则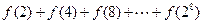 的值等于 .
的值等于 .