题目内容
已知函数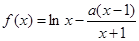 (
(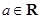 ,
,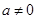 ),
),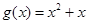 .
.
(1)求函数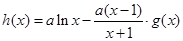 的单调区间,并确定其零点个数;
的单调区间,并确定其零点个数;
(2)若 在其定义域内单调递增,求
在其定义域内单调递增,求 的取值范围;
的取值范围;
(3)证明不等式  (
( ).
).
(1)当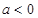 时,
时, 为
为 的减区间,
的减区间,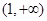 为
为 的增区间,
的增区间, 有且只有一个零点;当
有且只有一个零点;当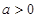 时,
时, 为
为 的增区间,
的增区间,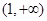 为
为 的减区间,
的减区间, 有且只有一个零点.
有且只有一个零点.
(2)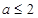 ;(3)祥见解析.
;(3)祥见解析.
解析试题分析:(1)首先求出已知函数的导数,然后由导数为正(为负)求得函数的增(减)区间,结合函数的单调区间就可求得函数的零点的个数;注意分类讨论;(2)由 在其定义域内单调递增,可知
在其定义域内单调递增,可知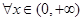 ,
,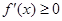 恒成立,从而就可利用二次函数的图象来求得字母的取值范围;或者分离参数将不等式的恒成立问题转化为函数的最值问题来加以解决;(3)观察所证不等式左右两边,联想已知的函数,由(2)可知 当
恒成立,从而就可利用二次函数的图象来求得字母的取值范围;或者分离参数将不等式的恒成立问题转化为函数的最值问题来加以解决;(3)观察所证不等式左右两边,联想已知的函数,由(2)可知 当 时,
时,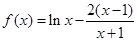 在
在 内单调递增,而
内单调递增,而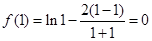 ,所以当
,所以当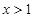 时,
时,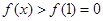 ,即
,即 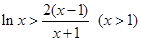 令
令 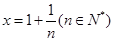 , 则
, 则  即:
即: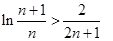
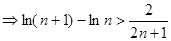 ,然后再令n=1,2,3,…,n得到n个式子,将这n个式子相加就可得到所证不等式.
,然后再令n=1,2,3,…,n得到n个式子,将这n个式子相加就可得到所证不等式.
试题解析:(1)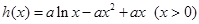 1分
1分
则 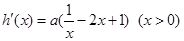
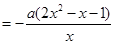
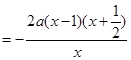 …2分
…2分
(i)若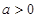 ,则当
,则当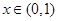 时,
时,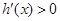 ;当
;当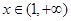 时,
时,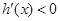
所以  为
为 的增区间,
的增区间,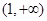 为
为 的减区间. 3分
的减区间. 3分
极大值为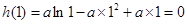
所以 只有一个零点
只有一个零点 .
.
(ii)若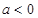 ,则当
,则当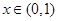 时,
时,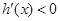 ;当
;当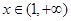 时,
时,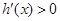
所以  为
为 的减区间,
的减区间,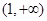 为
为 的增区间.
的增区间.
极小值为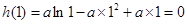 4分
4分
所以 只有一个零点
只有一个零点 .
.
综上所述,
当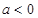 时,
时, 为
为 的减区间,
的减区间,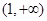 为
为 的增区间,
的增区间, 有且只有一个零点;
有且只有一个零点;
当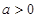 时,
时, 为
为 的增区间,
的增区间,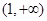 为
为 的减区间,
的减区间,
练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
 ______
______
 是定义在
是定义在 上的增函数,对于任意的
上的增函数,对于任意的 ,都有
,都有 ,且满足
,且满足 .
. 的值;
的值;  的
的 的取值范围.
的取值范围. .
. 在
在 上恒成立,求所有实数
上恒成立,求所有实数 ,证明:
,证明: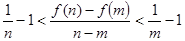
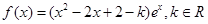 。
。 上的最小值为e,求k的值。
上的最小值为e,求k的值。 .
. 不可能为偶函数;
不可能为偶函数; 上单调递减的充要条件是
上单调递减的充要条件是 .
. 建市民健身广场,设计时决定保留空地边上的一水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中
建市民健身广场,设计时决定保留空地边上的一水塘(如图中阴影部分),水塘可近似看作一个等腰直角三角形,其中 ,
,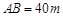 ,且
,且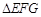 中,
中,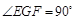 ,经测量得到
,经测量得到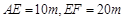 .为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点
.为保证安全同时考虑美观,健身广场周围准备加设一个保护栏.设计时经过点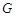 作一直线交
作一直线交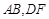 于
于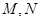 ,从而得到五边形
,从而得到五边形 的市民健身广场,设
的市民健身广场,设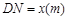 .
.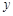 表示为
表示为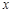 的函数;
的函数;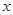 为何值时,市民健身广场的面积最大?并求出最大面积.
为何值时,市民健身广场的面积最大?并求出最大面积.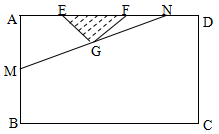
 ,g(x)=f(x)-ax,x∈[1,3],其中a∈R,记函数g(x)的最大值与最小值的差为h(a).
,g(x)=f(x)-ax,x∈[1,3],其中a∈R,记函数g(x)的最大值与最小值的差为h(a). 的图像如图所示,则
的图像如图所示,则 。
。