题目内容
某种产品的广告费支出 与销售额
与销售额 (单位:万元)之间有如下对应数据:
(单位:万元)之间有如下对应数据:
(1)求回归直线方程;
(2)试预测广告费支出为10万元时,销售额多大?
(3)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的绝对值不超过5的概率.
(参考数据:


参考公式:线性回归方程系数: ,
, )
)
 与销售额
与销售额 (单位:万元)之间有如下对应数据:
(单位:万元)之间有如下对应数据: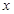 | 2 | 4 | 5 | 6 | 8 |
 | 30 | 40 | 60 | 50 | 70 |
(2)试预测广告费支出为10万元时,销售额多大?
(3)在已有的五组数据中任意抽取两组,求至少有一组数据其预测值与实际值之差的绝对值不超过5的概率.
(参考数据:



参考公式:线性回归方程系数:
 ,
, )
)(1) (2)销售收入大约为82.5万元(3)
(2)销售收入大约为82.5万元(3)
 (2)销售收入大约为82.5万元(3)
(2)销售收入大约为82.5万元(3)
试题分析:(1)首先求出x,y的平均数,利用最小二乘法做出线性回归方程的系数,根据样本中心点满足线性回归方程,代入已知数据求出a的值,写出线性回归方程.(2)当自变量取10时,把10代入线性回归方程,求出销售额的预报值,这是一个估计数字,它与真实值之间有误差.(3)利用列举法计算基本事件数及事件发生的概率 .本题考查回归分析的初步应用,考查求线性回归方程,考查预报y的值,是一个综合题目,解此类题,关键是理解线性回归分析意义,这种题目是新课标的大纲要求掌握的题型,是一个典型的题目,在近年的高考中频率有增高的趋势,此类题运算量大,解题时要严谨防止运算出错.
试题解析:(1)解:
 ,
, [2分]
[2分]又已知
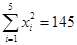 ,
,
于是可得:
 , [4分]
, [4分] 因此,所求回归直线方程为:
因此,所求回归直线方程为: [6分]
[6分](2)解:根据上面求得的回归直线方程,当广告费支出为10万元时,

 (万元) 即这种产品的销售收入大约为82.5万元. [9分]
(万元) 即这种产品的销售收入大约为82.5万元. [9分](3)解:
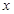 | 2 | 4 | 5 | 6 | 8 |
 |  30 30 | 40 | 60 | 50 | 70 |
 | 30.5 | 43.5 | 50 | 56.5 | 69.5 |
(60,50),(60,70),(50,70)共10个
两组数据其预测值与实际值之差的绝对值都超过5:(60,50) [12分]
所以至少有一组数据其预测值与实际值之差的绝对值不超过5的概率为
 [14分]
[14分]
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 ,
, )
) =3-5x,变量x增加一个单位时,y平均增加5个单位;
=3-5x,变量x增加一个单位时,y平均增加5个单位;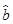 x+
x+ 必过(
必过( ,
, );
); 与支出
与支出 之间的关系大致符合
之间的关系大致符合 (单位:亿元),预计今年该城市居民年收入为20亿元,则今年支出估计是 亿元.
(单位:亿元),预计今年该城市居民年收入为20亿元,则今年支出估计是 亿元. (件)与销售价格
(件)与销售价格 (元/件)存在线性相关关系,根据一组样本数据
(元/件)存在线性相关关系,根据一组样本数据 ,用最小二乘法建立的回归方程为
,用最小二乘法建立的回归方程为 则下列结论正确的是( )
则下列结论正确的是( )  表示变量
表示变量
 的系数
的系数 ( )
( ) 



 ,若
,若 ,则
,则 .
.