题目内容
(本题满分12分,(Ⅰ)小问6分,(Ⅱ)小问6分.)
两个二次函数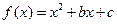 与
与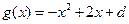 的图象有唯一的公共点
的图象有唯一的公共点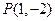 .
.
(Ⅰ)求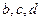 的值;
的值;
(Ⅱ)设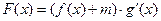 ,若
,若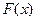 在
在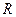 上是单调函数,求
上是单调函数,求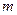 的范围,并指出是单调递增函数,还是单调递减函数.
的范围,并指出是单调递增函数,还是单调递减函数.
两个二次函数
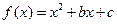 与
与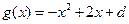 的图象有唯一的公共点
的图象有唯一的公共点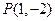 .
.(Ⅰ)求
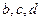 的值;
的值;(Ⅱ)设
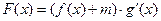 ,若
,若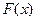 在
在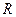 上是单调函数,求
上是单调函数,求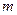 的范围,并指出是单调递增函数,还是单调递减函数.
的范围,并指出是单调递增函数,还是单调递减函数.解:(Ⅰ)由已知得 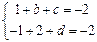 化简得
化简得 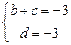 …………………2分
…………………2分
且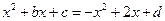
即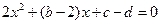 有唯一解 …………………………3分
有唯一解 …………………………3分
所以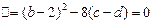 即
即 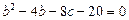
消去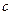 得
得 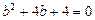 ,解得
,解得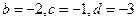 ………6分
………6分
(Ⅱ)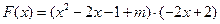
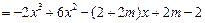 ……8分
……8分
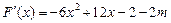 …………………………9分
…………………………9分
若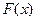 在
在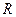 上为单调函数,则
上为单调函数,则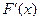 在
在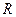 上恒有
上恒有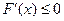 或
或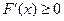 成立。
成立。
因为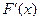 的图象是开口向下的抛物线,所以
的图象是开口向下的抛物线,所以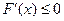 时
时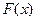 在
在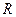 上为减函数
上为减函数
所以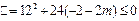 ,解得
,解得 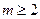
即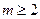 时,
时,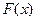 在
在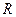 上为减函数。 …………………………12分
上为减函数。 …………………………12分
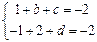 化简得
化简得 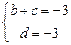 …………………2分
…………………2分且
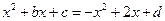
即
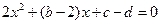 有唯一解 …………………………3分
有唯一解 …………………………3分所以
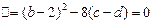 即
即 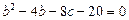
消去
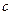 得
得 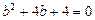 ,解得
,解得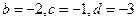 ………6分
………6分(Ⅱ)
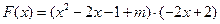
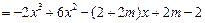 ……8分
……8分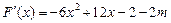 …………………………9分
…………………………9分若
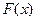 在
在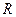 上为单调函数,则
上为单调函数,则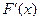 在
在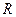 上恒有
上恒有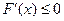 或
或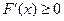 成立。
成立。因为
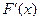 的图象是开口向下的抛物线,所以
的图象是开口向下的抛物线,所以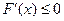 时
时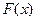 在
在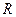 上为减函数
上为减函数所以
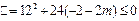 ,解得
,解得 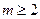
即
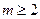 时,
时,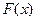 在
在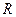 上为减函数。 …………………………12分
上为减函数。 …………………………12分略

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 ,则
,则
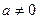 ,函数
,函数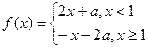 ,若
,若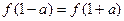 ,则a的值为________。
,则a的值为________。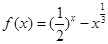 零点的取值范围是
零点的取值范围是



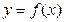 是函数
是函数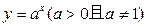 的反函数,且
的反函数,且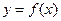 的图象过点(2,1),则
的图象过点(2,1),则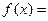 _____
_____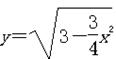 的图像上至少存在不同的三点到(1,0)的距离构成等比数列,则公比的取值范围_____________
的图像上至少存在不同的三点到(1,0)的距离构成等比数列,则公比的取值范围_____________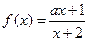 在区间
在区间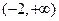 上是增函
上是增函 数,则实数
数,则实数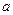 的取值范围
的取值范围  ,则满足
,则满足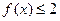 的
的 的取值范围是 ▲ .
的取值范围是 ▲ .