题目内容
设M是含有n个正整数的集合,如果M中没有一个元素是M中另外两个不同元素之和,则称集合M是n级好集合,
(Ⅰ)判断集合{1,3,4,7,9}是否是5级好集合,并写出另外一个5级好集合,满足其最大元素不超过9;
(Ⅱ)给定正整数a,设集合M={a,a+1,a+2,…a+k}是好集合,其中k为正整数,试求k的最大值,并说明理由;
(Ⅲ)对于任意n级好集合M,求集合M中最大元素的最小值(用n表示).
(Ⅰ)判断集合{1,3,4,7,9}是否是5级好集合,并写出另外一个5级好集合,满足其最大元素不超过9;
(Ⅱ)给定正整数a,设集合M={a,a+1,a+2,…a+k}是好集合,其中k为正整数,试求k的最大值,并说明理由;
(Ⅲ)对于任意n级好集合M,求集合M中最大元素的最小值(用n表示).
(I)∵1+3=4∈M,∴M不是5级好集合.
集合{1,3,5,7,9}是5级好集合.
(II)若a=1,则只能是M={1,2};
若a=2,则只能是{2,3,4};
若a=3,则只能是{3,4,5,6};…;
以此类推,只能是M={a,a+1,…,2a},因此k的最大值为2a-a=a.
(III)对于任意n级好集合M,集合M最大元素的最小值为2n-2.
若最大元素为2n-3,将{1,2,…,2n-3}分为:
t=(2n-3),
t1=(1,2n-4),
t2=(2,2n-5),
…
tn-2=(n-2,n-1).
则显然t1~tn-2这n-2组中每一组至多选择一个数,
故此时M中的运算个数至多为n-2+1=n-1<n,故当最大元素为2n-3时,不能取得M.
同理可证最大元素<2n-3时不满足题设条件.
当最大元素为2n-2时,取M={n-1,n,n+1,n+2,…,2n-2}.则此集合对任意n满足题意.
综上可知:对于任意n级好集合M,求集合M中最大元素的最小值为2n-2.
集合{1,3,5,7,9}是5级好集合.
(II)若a=1,则只能是M={1,2};
若a=2,则只能是{2,3,4};
若a=3,则只能是{3,4,5,6};…;
以此类推,只能是M={a,a+1,…,2a},因此k的最大值为2a-a=a.
(III)对于任意n级好集合M,集合M最大元素的最小值为2n-2.
若最大元素为2n-3,将{1,2,…,2n-3}分为:
t=(2n-3),
t1=(1,2n-4),
t2=(2,2n-5),
…
tn-2=(n-2,n-1).
则显然t1~tn-2这n-2组中每一组至多选择一个数,
故此时M中的运算个数至多为n-2+1=n-1<n,故当最大元素为2n-3时,不能取得M.
同理可证最大元素<2n-3时不满足题设条件.
当最大元素为2n-2时,取M={n-1,n,n+1,n+2,…,2n-2}.则此集合对任意n满足题意.
综上可知:对于任意n级好集合M,求集合M中最大元素的最小值为2n-2.

练习册系列答案
相关题目
 为三角形
为三角形 的三边,求证:
的三边,求证:
 的前
的前 项和为
项和为 ,则
,则 ,
, ,
, ,
, 成等差数列.类比
成等差数列.类比 的前
的前 ,则
,则 , ,
, , 成等比数列.
成等比数列.
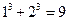 ; ⑵
; ⑵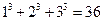 ;⑵
;⑵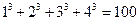 ,
, .
. 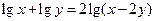 ,则
,则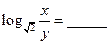 。
。